Snijpunten van een cirkel en een lijn

In de ligging van de lijn y = ax+b (lineair) ten opzichte van de cirkel x² + y² = r² zijn drie gevallen te onderscheiden:

1. de lijn y = ax+b snijdt de cirkel in 2 punten
2. de lijn y = ax+b snijdt de cirkel in 1 punt
3. de lijn y = ax+b snijdt de cirkel niet

Opdracht:

Bedenk in ieder van deze 3 situaties een vergelijking voor de cirkel en de lijn. Toon m.b.v. deze vergelijkingen, gebruik makend van de discriminant, aan dat er sprake is van 2, 1 of geen enkel snijpunt.
Ik heb geen idee hoe ik deze opdracht moet maken.

Daniël
Leerling bovenbouw havo-vwo - zondag 6 april 2008

Antwoord

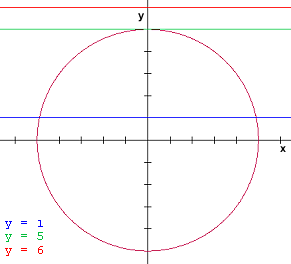
Neem bijvoorbeeld x²+y²=25. Dat is een cirkel met middelpunt O(0,0) en r=5. Er geldt dan (bijvoorbeeld:

1. De lijn y=0 snijdt de cirkel in twee punten.
2. De lijn y=5 snijdt de cirkel in één punt.
3. De lijn y=6 snijdt de cirkel niet.



Zal ik nog even laten zien hoe dat zit met die dicriminant? Nou vooruit maar...

x²+y²=25 en y=5, er geldt: x²+25=25, dus x²=0. De discriminant van deze vergelijking is inderdaad gelijk aan 0. Dus 1 snijpunt...

Flauw hè?

Ander voorbeeld dan maar?

We snijden de cirkel met vergelijking x²+y²=25 met de lijn met vergelijking y=-³/₄x+6¹/₄.



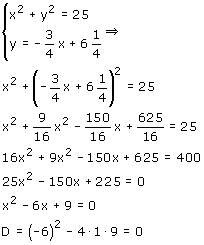
De discriminant is nul, dus er is precies één snijpunt. Dus, zoiets dus...

zondag 6 april 2008

Re: Snijpunten van een cirkel en een lijn

©2001-2024 WisFaq