Steinerboom

Mijn vraag aan u betreft het onderwerp steiner netwerken. De kortste verbinding van drie willekeurige punten volgt uit een constructie met het punt van Fermat. Het verbinden van vier punten lukt ook door middel van een constructie. Maar mijn vraag is nu hoe men 5 of meer punten met elkaar moet verbinden (de kortste verbinding) aan de hand van deze kennis. In allerlei boeken kwam ik dingen tegen over algoritmen en heuristieken; maar dat begreep ik niet. Ik heb een vermoeden dat je de punten in groepjes moet verdelen en van deze groepjes afzonderlijk de steinerpunten moet bepalen. Om vervolgens van deze punten een geheel te vormen. Ook moet ik isolijnen construeren; maar ik begrijp niet wat dit precies met steiner-netwerken te maken heeft. Bij voorbaat zeer bedankt.

Eric Z
Student hbo - donderdag 28 februari 2008

Antwoord

Beste Eric,
Bij de constructie van de kortste boom met 3 punten, waar een Steiner punt aan is toegevoegd zie je dat de hoeken tussen de lijnen steeds 120 graden zijn.
Dat is ook het geval als je met meer punten begint.
In het algemeen zal je bij n punten n-2 Steiner punten moeten kiezen.

Voor 4 punten kan je die op twee manieren construeren, afhankelijk van welke hoekpunten je selecteert :
Bijvoorbeeld in vierhoek ABCD kan je gelijkzijdige driehoeken tekenen op AB en CD, maar ook op BC en AD.Een van de twee levert de kortste verbinding op.
Berekening waar je de Steiner punten moet kiezen is niet makkelijk. Er zijn computerprogramma's voor.

Een mooi voorbeeld is:

http://space.geocities.jp/flashr0d/steinertree.html

Dit is gebaseerd op het volgende experimentele principe:
Maak in een plankje gaatjes bij de hoekpunten.
In onderstaand voorbeeld: A,B,C,D en E.
Je wil 3 Steiner punten bepalen. selecteer twee hoekpunten en trek een touwtje door de gaatjes bij die twee hoekpunten . Aan de uiteinden van dat touwtje hangen gelijke gewichtjes.Trek nu ook touwtjes door de overige gaatjes. Die zitten met ringetjes om het eerste touwtje en hebben ook gewichtjes aan de uiteinden onder het plankje. (Misschien een wat warrig verhaal, maar onderstaand plaatje zal het wel verduidelijken).


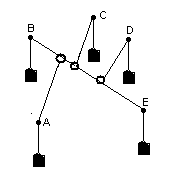
De ringetjes vormen de Steiner punten.
Laat nu de gewichtjes hun werk doen en je krijgt in ieder geval een lokaal minimum. Door de juiste punten te selecteren kan je het echte minimum vinden.

Dan je vraag over isolijnen:
Dat kan mijns inziens alleen met drie punten:
Kies een vierde punt op een willekeurig plaats, verbindt dit met de drie hoekpunten en bereken de totale weglengte.
Doe dit bijvoorbeeld voor alle roosterpunten en schrijf dan die afstand bij het roosterpunt.
Verbindt nu roosterpunten met gelijke afstanden met elkaar en je hebt een isolijn.

Hoop dat dit ongeveer is wat je zocht.
Groet, Lieke.

ldr
vrijdag 7 maart 2008

©2001-2024 WisFaq