Oppervlakte berekenen

Goedemiddag,
Het betreft een vraag over een oppervlakte berekening van een stuk land. Er zijn 4 verschillende afmetingen, daar het stuk land niet rechthoekig is!
De afmetingen zijn:
A: 121,20m - B: 26,65m - C: 88,45m - D: 47m
Er wordt mij verteld dat de totaaloppervlakte 3.860 m2 bedraagt. Kunt u mij uitleggen of dit wel klopt?
Tevens lijkt het mij een geschikte vraag voor uw mede-leerlingen!
Hopende dat u mij met deze vraag kunt helpen!
Met vriendelijke groeten...

Jeffre
Ouder - donderdag 14 november 2002

Antwoord

Hoi,

Hier kan je dezelfde logica toepassen als in Graden & hoeken.

We veronderstellen dat de lengtes A,B,C en D aansluitend zijn tussen respectievelijk punten a,b,c en d. We hebben dus: |ab|=A, |bc|=B, |cd|=C en |da|=D.
We noemen |ac|=t

Dan moet ||ab|-|bc||t|ab|+|bc| en ||ad|-|dc||t|ad|+|dc|.
Rekening houdend met de effectieve waarden van A,B,C en D:
A-BtC+D [1].

In functie van t kunnen we ook de oppervlakte van driehoeken abc en adc berekenen met de formule Opp²=s.(s-x).(s-y).(s-z) waarbij x,y en z de lengte van de zijden zijn en s de halve omtrek.
Voor elke driehoek is de oppervlakte dus de vierkantswortel van een veeltermfunctie in t. De totale oppervlakte f(t) is dus de som van twee vierkantswortels uit veeltermfuncties in t. Om de t-waarde te berekenen bij gegeven oppervlakte S, moeten we dus f(t)=S oplossen.

f(t) heeft echter volgend verloop:



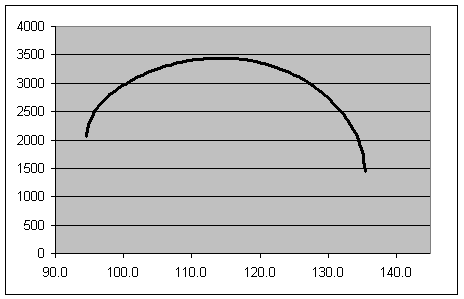
Het zou dus wel interessant kunnen zijn om de maximale waarde van f(t) te bepalen (f'(t)=0 ergens rond t=114; je kan dit op de grafiek zien of numerisch narekenen)...

Als je nog hulp nodig hebt, laat je het maar weten.

Groetjes,
Johan

andros
donderdag 14 november 2002

©2001-2024 WisFaq