Capita Selecta van de Analyse

D is de driehoek in het x,y-vlak met hoekpunten (0,0), (0,1)en (1,1). V is het lichaam in de x,y,x-ruimte, begrensd door de platte vlakken x=0, y=1, x=y en z=0, en de paraboloïde z=4-x²-y².

Vragen hierbij:
1. Teken V.
2. Laat zien dat de inhoud van V gelijk is aan de Dubbelintegraal (over D) (4-x²-y²)dx dy.
3. Bereken de inhoud van V.

E.T.M.
Student hbo - woensdag 13 november 2002

Antwoord

Beste E.T.M. Jacobs,

Je wilt dus uiteindelijk de inhoud van V bepalen op het gebied begrenst door D. Met D als driehoek en V als parabloïde.
Als eerste vraag je naar de tekening. Dit kan je als beste als volgt doen:
a) Stel y=0 en bereken enkele punten voor x en z
b) Stel x=0 en bereken enkele punten voor y en z
Teken deze punten en maak er een mooie 3d tekening van.
Je krijgt dan als het goed is iets als hieronder:



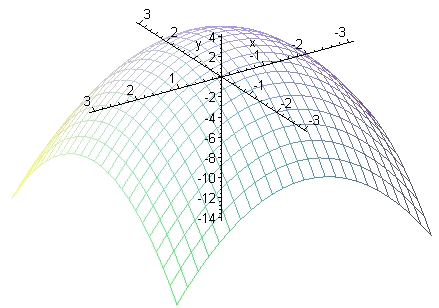
Teken in dezelfde grafiek ook de driehoek.
Verder moet je nog de inhoud van V berekenen op het gebied van:
x = 0..1, maar pas op
y = 0..x
Want als x=0,5 dan geldt ook dat y=0,5.
Dus we krijgen dan:
òò4-x²-y² dy dx
Dus:
ò(ò4-x²-y² dy, y=0..x) dx
Eerst het gedeelte tussen haakjes:
ò4-x²-y² dy, y=0..x = 4y-yx²-¹/₃y³ | y=0..x
= 4x-x³-¹/₃x³ - 0
= 4x-x³-¹/₃x³
= 4x-1¹/₃x³
Invullen en we houden over:
ò4x-1¹/₃x³ dx, x=0..1 =
2x²-¹/₃x⁴ | x=0..1 =
2·1³-¹/₃·1³ - ¹/₃·0³=
2-¹/₃=1²/₃

Hopelijk heb je hier wat aan.

M.v.g.

zaterdag 16 november 2002

©2001-2024 WisFaq