
Steekproefvariantie
Er is sprake van de volgende populatiex p(X=x)
0 0,6
2 0,3
4 0,1 Uit deze populatie wordt een aselecte steekproef getrokken van omvang 2, x1 en x2.
Vervolgens moet je de de T (steekproeftotaal), m (steekproefgemiddelde), s2 (steekproefvariantie) en de s (steekproefstandaardafwijking) berekenen.
Ik weet hoe ik de kans moet berekenen en het totaal
dan kom ik uit op het volgende schema:steekproef kans t m
0,0 0,36 0 0
0,2 0,18 2 1
0,4 0,06 4 2
2,0 0,18 2 1
2,2 0,09 4 2
2,4 0,03 6 3
4,0 0,06 4 2
4,2 0,03 6 3
4,4 0,01 8 4 Maar nu begrijp ik totaal niet hoe ik de s2 moet uitrekenen.. door het antwoordblaadje weet ik bijv. dat de s2 van 2,0 = 2.. maar hoe kom je aan dit antwoord?
Alvast heel erg bedankt
amber
Student universiteit - zondag 25 november 2007
Antwoord
Je kunt de verwachtingswaarde en standaarddeviatie met je GR berekenen:
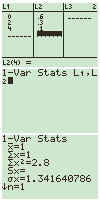
Maar dat kan ook 'met de hand':

We stellen vast:
E(X)=1
s(X) 1,34 1,34
Je bent natuurlijk bekend met de wortel-n wet!?
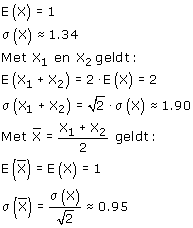
...en dan ben je er wel zo'n beetje...
Ik begrijp alleen niet wat die tweede tabel is. Hoe kom je daar aan? En wat is het?

zondag 25 november 2007
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|