Afleiden formule oppervlakte afgeknotte kegel

Hallo,
Ik heb jullie hulp nodig. Vandaag kreeg ik m'n toets wiskunde te zien (cijfer: 6,1 telt ook mee voor examen). We moesten de oppervlakte van de mantel van een lampen kap berekenen. Dit heb ik gedaan met de volgende formule:





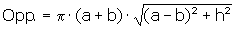
Ik had het antwoord (en de berekening dus ook) goed, maar mijn wiskundeleraar kende de bovenstaande formule niet. Ik heb er dus geen punten voor gekregen (anders had ik een 7). Nu wil hij weten hoe en waarvan die formule is afgeleid. Dan krijg ik misschien mijn punten wel. Ik kwam er zelf niet uit en kon het ook niet op internet vinden. Zou een van jullie de formule van de oppervlakte van een afgeknotte kegel kunnen afleiden? Bij voorbaat dank!

Jochem
Leerling bovenbouw havo-vwo - woensdag 21 november 2007

Antwoord

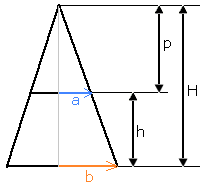
In alle leerboeken wordt voor de manteloppervlakte van een kegel de formule $\pi$.r.R gebruikt, en die zal dan ook wel in jouw boek te vinden zijn. Hierin is r de straal van de grondcirkel en R is de afstand van de top van de kegel naar het grondvlak. Die afstand wordt wel het apothema genoemd en in jouw tekening is dat de schuine zijde van de grote driehoek.

Nu wat jouw formule betreft. De wortelvorm is gewoon de lengte van de schuine zijde van de onderkant van de afgeknotte kegel. Om geen misverstanden te krijgen: het is de afstand tussen de blauwe en de gele pijlpunt in je tekening en de verklaring is simpel: Pythagoras.

Als we die afstand aanduiden met de letter d, dan is de lengte van de schuine zijde in jouw bovenste driehoek (dus van de top naar de blauwe pijlpunt) gelijk aan ad/(b-a). Dit kun je inzien door op te merken dat de verhouding tussen onder en boven a:b is. Laten we die afstand even aanduiden met D.

De manteloppervlakte van de afgeknotte kegel wordt dan op grond van de eerste opmerking: $\pi$.(D+d).b - $\pi$.D.a = $\pi$.D.(b-a) + $\pi$.d.b
Vervang je nu D door ad/(b-a), dan wordt het voorgaande $\pi$.a.d + $\pi$.b.d = $\pi$.(a+b).d en door ten slotte d te vervangen door die wortelvorm uit je formule, ben je er.

Ik geef je leraar overigens gelijk: de formule die jij hanteert staat niet op het formuleblad en dús mag je hem niet zomaar gebruiken.
Hopelijk krijg je toch nog je 7 en vergeet je niet om Wisfaq te vermelden.

MBL

MBL
woensdag 21 november 2007

Re: Afleiden formule oppervlakte afgeknotte kegel

©2001-2024 WisFaq