
Re: Re: Systeem bestaande uit samenhangende formule`s
Beste Oscar,
G bijwerken op een zelf te kiezen moment, ten koste van E. Het doel is om ze snel mogelijk een bepaalde waarde van G te bereiken. Het is waarschijnlijk nuttiger om eerst een hoeveelheid E te spenderen aan formule's die vermeerderen (bijv. C).
Du en Eu willen eigenlijk alleen maar zeggen dat je een hoeveelheid van D of E gebruikt aan een bepaalde andere formule (bijv. G). Dit gebeurt dan ook op het moment dat de 'hoofd formule' wordt bijgewerkt (voor G is dit dus een vrij te kiezen moment). Hoeveel je spendeerd van D of E is ook vrij te kiezen. Met als uitzondering bijv. de formule voor C waar D meervoude van 100.000 moet zijn en E meervouden van (50/F).
Het gaat dus eigenlijk om de volgende vragen om zo snel mogelijk een bepaalde waarde van G te krijgen:
1. Welke formule wanneer uitvoeren. (die vrij te kiezen zijn)
2. Welke hoeveelheid D en E gebruiken.
Alle getallen zijn hele getallen (integers).
Afronden van B is eigenlijk zinloos omdat het hele getallen zijn. De formules waar floor wordt gebruikt (A, C en F). Is omdat deze gaan met bepaalde 'stappen'. Bijvoorbeeld de stappen van A zijn 0, 50, 100. Als het dan bijvoorbeeld 75 is dan geld de stap van 50.
Hieronder wat voorbeelde, waar ik tot de ontdekking kwam dat ik de formule voor A verkeerd had genoteerd. Dit kwam omdat ik eerst C nog niet in stapgroottes van 50 had laten verlopen omdat dit bij A gedaan werd. Nu dit echter bij C al wordt gedaan. Wordt de formule voor A: A=A+C en daarmee eigenlijk geheel overbodig. Toch zal ik hem nog wel gebruiken in het voorbeeld.
Ook kwam ik erachter dat de formule voor G moest zijn: G = G + A*Eu. Excuseer.
Bij de volgende voorbeelden is het doel om G tot 200 te krijgen. Dit is een eenvoudig voorbeeld. Bijna altijd zal G veel groter zijn (met maximum van 11000 ongeveer). Hoe groter G wordt hoe nuttiger het wordt om de formule B en/of F uit te voeren zodat C ook weer gedaan kan worden.
Voorbeeld 1:
t=0: Startwaardes: A=1, B=1000, C=0, D=10000, E=100, F=5, G=0
t=0: Voer uit G (met A):
A = A + C = 1 + 0 = 1
G = G + A * Eu = 0 + 1 * 100 = 100
E = E - Eu = 100 - 100 = 0
t=25: In deze tijd is E 25x uitgevoerd, na deze tijd op t=25 wordt G uitgevoerd:
E = E + 4  -- 25x (ook wel E=E+4t). E wordt 100 -- 25x (ook wel E=E+4t). E wordt 100
G = G + A*Eu = 100 + 1*100 = 200
E = 100 - 100 = 0
Resultaat: G=200 bereikt bij t=25
Voorbeeld 2:
t=0: Startwaardes: A=1, B=1000, C=0, D=10000, E=100, F=5, G=0
t=0: Voer uit C:
Eu=10, Du=100000, F=5
floor(Eu / (50/F)) = floor (10 / (50/5)) = 1
floor(Du/100000) = floor(100000/100000) = 1
C = C + 1 = 0 + 1 = 1
E = E - Eu = 100 - 10 = 90
D = D - Du = 100000 - 100000 = 0
t=0: Voer uit G (met A):
A = A + C = 1 + 1 = 2
G = G + A * Eu = 0 + 2 * 90 = 180
E = E - Eu = 90 - 90 = 0
t=3: E is 3x uitgevoerd, op t=3 voer G uit:
E = E + 4  -- 3x (ook wel E=E+4t). E wordt 12 -- 3x (ook wel E=E+4t). E wordt 12
G = G + A*Eu = 180 + 2*10 = 200
E = 12 - 10 = 2
Resultaat: G=200 bereikt bij t=3
Ik heb het er voor over om zelf een algoritme te schrijven. Dit heb ik al gedaan alleen het werkte niet goed en bepaalde zaken waren er nog niet in opgenomen. Een genetisch algoritme ken ik niet.
Flip
Student hbo - zaterdag 17 november 2007
Antwoord
Beste Flip,
Als ik heel eerlijk ben wordt ik niet erg enthousiast van jou vraag. Ik zie een stel ingewikkelde regels van een spel dat me verder niets zegt en moet dan gaan zoeken naar een optimale strategie. Dat zal zeker een heleboel rekenwerk zijn (anders is het een simpel spel).
Hieronder wil ik nog wel met wat voorbeelden laten zien hoe je dit probleem aan kunt pakken. Maar als je echt een oplossing wilt zul je het echt zelf moeten doen. Natuurlijk is het prima als je de vraag nog een keer indient. Misschien wordt een van mijn collega's enthousiaster. Maar, ik denk het niet.
Welnu. Ik zal er maar vanuit gaan dat je de optimale oplossing met een computer moet zoeken. Dan moet je twee zaken doen. Eerst zul je de regels zo in moeten voeren dat de computer zelf het spel kan spelen. Dat is op zich prima te doen. Maar je zal ook een manier moeten vinden om de strategie vast te leggen.
========================= SIMULEREN =============================
Laat ik dit eens illustreren met een eenvoudig spel als voorbeeld. Dit spel gaat als volgt. Je hebt een bankrekening waar iedere beurt 3 euro op wordt gestort. Aanvankelijk is de rente 0%. Maar, iedere beurt kun je een deel van je banksaldo gebruiken om rente te kopen. Voor iedere euro gaat de rente (permanent) met 1% omhoog. Je hebt een aantal beurten om zo veel mogelijk geld op de bank te krijgen.
Dit spel is niet zo realistisch, maar het heeft een ietwat niet-triviale strategie. Je kunt je geld steeds meteen gebruiken om de rente te verhogen. Maar dan krijg je nergens rente over. Je kunt ook een tijdje sparen om vervolgens in één keer meer rente te kopen.
Even een paar voorbeeldjes. Eén mogelijkheid is om alles op je rekening te laten staan en geen rente te kopen. Het verloop in de eerste vier beurten is dan:
saldo: 3 6 9 12
rente: 0,0 0,0 0,0 0,0
Het saldo loopt wel op, maar je hebt geen rente. Dat maakt in de eerste vier beurten ook niet uit, maar op termijn zal dit toch niet optimaal zijn. Een variatie is: in de vierde beurt rente kopen. Het verloop is dan:
saldo: 3 6 9 3
rente: 0,0 0,0 0,0 9,0
Je hebt dan na 4 beurten niet zoveel geld, maar wel een flinke rente. Dus in een aantal beurten zal je rente zoveel bijdragen dat je meer hebt dan bij de eerste strategie.
Een andere mogelijkheid is: in iedere beurt een deel van je geld gebruiken om rente te kopen. Als dat steeds de helft is is het verloop:
saldo: 3 4,5 5,28 5,74
rente: 0,0 1,5 3,8 6,4
Je hebt na vier beurten meer geld maar minder rente dan bij de vorige strategie. De vraag is (net als bij jouw spel) bij welke strategie heb je nu de hoogste opbrengst.
Maar goed. Hoe laat je de computer zoiets uitrekenen. Je moet dan per beurt het saldo en de rente bijhouden. Maar je zult ook (per beurt) moeten vastleggen welk deel van het saldo je in iedere beurt gebruikt om rente te kopen. Dit alles gaat met drie array's een een stel recursievergelijkingen.
verdeling[t] kies je zelf voor elke waarde van t.
saldo[0]=3; rente[0]=0;
saldo[t+1] = verdeling*saldo[t]*(1+rente[t]/100)+3;
rente[t+1] = rente[t]+(1-verdeling[t])*saldo[t];
Je kunt dit algoritme in allerlei computerprogramma's uitvoeren. Het kan bij voorbbeeld ook in excel. Je maakt dan één rij met alle keuzes voor verdeling[t], één rij voor saldo[t] en één voor rente[t]. In deze laatste twee rijen zet je op de eerste plek de beginwaarden en op alle andere plekken een formule om de volgende waarde uit te rekenen. In het volgende plaatje zie je ongeveer hoe dat gaat:
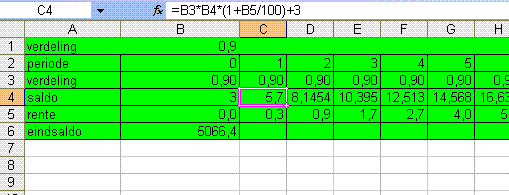
Op het plaatje zie je ook het eindsaldo (op t=24). In dit voorbeeld heb ik steeds 10% van het saldo besteed aan het kopen van rente. Dat levert uiteindelijk 5000 euro op. Veel meer dan wanneer je alles op het saldo laat staan. De meeste optimale strategie is om in iedere beurt 16,7% van je saldo aan rente te besteden. Het eindsaldo is dan 14500 euro.
================== OPTIMALISEREN ==================
Maar, kun je nog meer verdienen door per beurt een verchillend deel van je geld aan rente te besteden? Daarmee kom ik bij het tweede probleem dat ook jij op moet lossen. Je hebt je strategie vastgelegd met 24 getallen (verdeling[0] t/m verdeling[23]). Voor welke keuze van de getallen is je eindsaldo het hoogst. Nu zul je een optimalisatiealgoritme moeten bedenken.
Dit heeft weinig meer met het spel te maken. Het probleem is gewoon als volgt: Je hebt een functie f() met 24 variabelen: y=f(x0,x1,...,x23) voor welke waarden van x0, x1, ..., x24 is y het grootst?
Je kunt dit uitzoeken door steeds één van de variabelen een stukje te veranderen en te kijken of y groter wordt of juist kleiner. In het laatste geval moet je de andere kant op.
Maar hoeveel moet je de variabelen veranderen. De eenvougiste aanpak is de gradient-search. Je bepaalt eerst de gradient van de functie. Dat is de vector {g0,g1,...g23} met gn = df/dxn. Deze gradient geeft de richting aan waarin de functie het snelst afneemt. Nu ga je je vector {x0,x1,...,x23} in die kant varanderen. Dit kan alsvolgt:
x0'=x0+schaalfactor*g0
x1'=x1+schaalfactor*g1
.
.
.
x23'=x23+schaalfactor*g23
g0'=(f(x0'+g0,x1',...x23')-f(x0',x1',...x23'))/g0
g1'=(f(x0',x1'+g1,...x23')-f(x0',x1',...x23'))/g1
.
.
.
g23'=(f(x0',x1',...x23'+g23)-f(x0',x1',...x23'))/g23
De schaalfactor is nodig om de parameters niet te snel te veranderen. Als je de schaalfactor groot kiest, wandelt het algoritme met grote stappen maar is de kans groot dat je het optimum voorbijschiet. Als je de schaalfactor heel klein kiest kom je (bijna) altijd bij het optimum maar het kan wel heel lang duren.
Dit optimaliseringsalgoritme heb ik ook in excel geimplementeerd. Maar, ik heb het wel een beetje anders gedaan. Het probleem is namelijk dat je voor het bovenstaande 24 keer de waarde van f( ) uit moet rekenen. Aangezien ik iedere keer een simulatie van het spel moet uitvoeren wordt me dat te ingewikkeld. Ik kies ervoor om na iedere simulatie één variabele te veranderen en ook de bijbehorende gradient.
Als je me een e-mail stuurt (somsen-nacion@planet.nl) kan ik je de excelfile sturen. Maar, het gaat ongeveer als op dit plaatje.
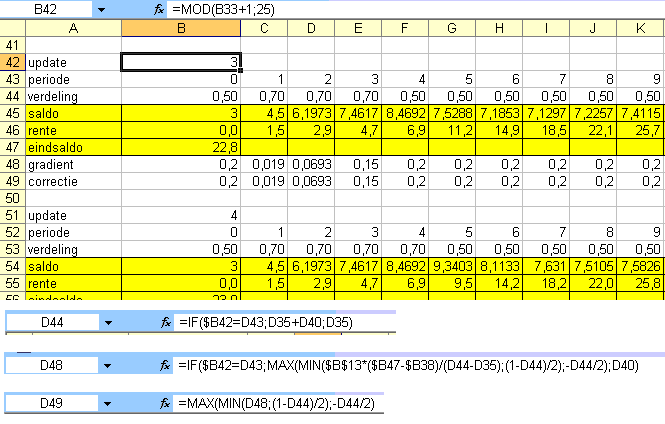
Achter de rijen waarin je het spel simuleert maak je nog een rij waarin je de gradient beweert. In het plaatje zie je de formule waarmee je besluit welke van de verdelingsvariabelen je in deze ronde gaat updaten. Onderaan zie je dan de formules waarmee je de nieuwe waarde van de variabele en de gradient berekent. Er is nog een correctie nodig om ervoor de zorgen dat de verdeling niet kleiner dan 0 wordt of groter dan 1.
Als je dit stukje code eenmaal gemaakt hebt kun je het net zo vaak kopieren als je wilt. Ik heb dat 240 keer gedaan. De excelfile voert dan 240 optimalisaties uit zodat elke variabele 10 keer geupdate wordt. Maar je kunt ook duizenden stappen in één keer doen. Alleen wordt je file dan wel groot. Het verloop zag er alsvolgt uit:
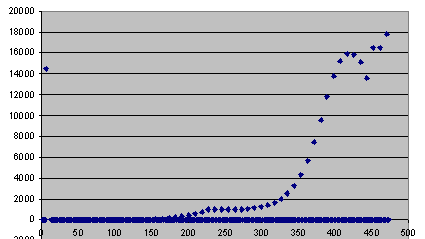
In deze simulatie vindt ik al een strategie die meer oplevert dan de constante verdeling, nl 18000 euro. De bijbehorende verdeling was:
optimum 0,35 0,71 0,76 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85 0,85
Dus: In de eerste stap 65% van je saldo aan rente besteden. Daarna snel minder tot een constant percentage van 15%. Maar dit is zeker niet de beste oplossing. Ik heb ook oplossingen gevonden die ongeveer 25000 euro opleveren.
Nu nog wat opmerkingen:
* Met dit werk ben ik ongeveer een halve dag bezig geweest. Eenvoudig is het dus niet. Maar, wat jij wilt is nog een heel stuk ingewikkelder.
* Het gradientalgoritme is zeker niet het beste. Als je het uitprobeert zul je zien dat je je optimum toch snel voorbijschiet. Of je moet de schaalfactor zo klein maken dat je er nooit komt. Er zijn veel betere algoritmes, maar die zijn ook veel moeilijker te programmeren. Als je je er in verdiept en een betere programmeertaal (bij voorbeeld java of C) gebruikt kun je veel betere resultaten halen. De conjugate-gradient-methode is al een stuk beter. Voor dit probleem denk ik dat een genetisch algoritme het meest geschikt is. Maar, daar heb je echt specialistische software voor nodig.
* En tenslotte: Hoe weet je nu wanneer je echt de optimale oplossing hebt gevonden? Als alle waarden van de gradient nul worden zijn ook alle afgeleiden van f() gelijk aan nul. Dan heb je het (of in ieder geval een) optimum gevonden.
Groet. Oscar
======================== PS ===========================
Toch nog even over jouw spel. Je zit met iets vergelijkbaars. Je wilt G zo hoog mogelijk hebben. Je kunt gewoon wachten tot E hoog genoeg is, maar dat is (zoals jij zelf als zegt) niet heel efficient. Je kunt ook proberen A hoger te krijgen. Dat vergelijkbaar met het kopen van rente in mijn voorbeeld. Alleen gaat het verhogen van A op een buitengewoon ingewikkelde manier via B, C, D en F. Bovendien moet jij per beurt niet één keuze maken, maar een aantal (welke updaten? B, C, D of F? En met hoeveel?). Ik zie er nog altijd geen been in. Maar het optimum zal iets vergelijkbaars zijn: af een toe een deel van je saldo gebruiken om één van de variabelen op te hogen. En dat deel zal langzaam verschuiven in de loop van het spel. Maar hoe? Daar zie ik nog altijd geen been in. Er moet je wel bijzonder veel aan gelegen zijn om dat uit te willen zoeken.
======================== PPS =========================
Wellicht is er nog wat licht op je schema te werpen door het te vereenvoudigen. Op dit moment is onduidelijk welke variabelen het belangrijkst zijn omdat sommigen heel groot zijn en anderen heel klein. Dat kun je veranderen als je de afronding weglaat (het systeem wordt dan natuurlijk wel anders)
stap 1: Afronding weglaten:
start: A=1, B=1000, C=1, D=100000, E=100, F=5
keuze: C = C + gelijk(F*Eu/50,Du/100000) (E=E-Eu, D=D-Du)
A = C/50
keuze: B = B + A*Eu*1000 (Bmax=500000, E=E-Eu)
keuze: F = F + A*Eu/200 (Fmax=15, E=E-Eu)
altijd: D = D + B
altijd: E = E + 4
G = A*Eu (E=E-Eu)
stap 2: En B en D door 1000 delen:
start: A=1, B=1, C=1, D=100, E=100, F=5
keuze: C = C + alsgelijk(F*Eu/50,Du/100) (E=E-Eu, D=D-Du)
A = C/50
keuze: B = B + A*Eu (Bmax=50, E=E-Eu)
keuze: F = F + A*Eu/200 (Fmax=15, E=E-Eu)
altijd: D = D + B
altijd: E = E + 4
G = A*Eu (E=E-Eu)
stap 3: Nu A wegwerken, D en E door 100 delen en F door 5:
start: B=1, C=1, D=1, E=1, F=1
keuze: C = C + alsgelijk(10*F*Eu,Du) (E=E-Eu, D=D-Du)
keuze: B = B + 2*C*Eu (Bmax=50, E=E-Eu)
keuze: F = F + C*Eu/20 (Fmax=3, E=E-Eu)
altijd: D = D + B/100
alijd: E = E + 1/25
G = 2*C*Eu (E=E-Eu)
Als alles nu rond de 1 zit veranderen C en B redelijk snel maar F, D en E veel langzamer. Je kunt B (en dus ook D) snel laten groeien, maar C niet (want daar heb je E voor nodig).
* Het ligt (wellicht) voor de hand om E en D gelijk te laten groeien. Het heeft in ieder geval geen zin om D heel hard te laten groeien als je toch C niet kunt verhogen.
* Het ligt ook voor de hand om op G=10000 te komen door E en C allebei tot 100 te laten groeien. Tenzij het veel makkelijker is om een van beide te laten groeien.
* De groei van D kun je versnellen door eerst B te laten groeien. De groei van E kun je niet versnellen. Daardoor zou het kunnen zijn dat het toch beter is om C te laten groeien.
* Als B en F maximaal zijn groeit D 1/2 per beurt. C kan dus ook maximaal 1/2 per beurt stijgen. Als F ook maximaal moet Eu steeds 1/60 zijn. Je gebruikt dan ongeveer de helft van de groei van E om C op te hogen. E zelf stijgt dan nog met 1/25-1/60=1/40, dus 20 keer zo langzaam als C. Na 800 beurten is C=400 en E=20 zodat G=8000. Dan ben je er bijna. Als B en F maximaal zijn heb je dus nog 800 beurten nodig.
os
maandag 19 november 2007
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|