Waarom is sin(2pi/3) equivalent met sin(pi/3)?

Waarom geldt:
sin(2p/3) = sin(p/3) = ¹/₂Ö3
sin(3p/2) = -sin(p/2)= -1
sin(7p/4) = -sin(p/4)= -¹/₂Ö2
Waar blijven de 2,3 en 7?En geldt dat getal 2 dan negatief?

Barry
Leerling bovenbouw havo-vwo - maandag 17 september 2007

Antwoord

Beste Barry,

Je kan kijken naar de eenheidscirkel, waarin je lijnen tekent door de oorsprong, met hoeken 2p/3 en p/3 met de positieve x-as. (tegen de klok in).
Dat is dus in graden: 120⁰ en60⁰.
Je ziet dan dat die lijnen de cirkel op gelijk hoogte snijden.
Je weet ook dat de sinus van die hoeken overeenkomt met de hoogte, of de y-coördinaat van de snijpunten met de cirkel.

Een andere manier is om te kijken naar de grafiek van sin(x).
Ook dan zie je dat de y-coördinaat bij 2p/3 en p/3 gelijk is.
Het beste is natuurlijk om allebei de methodes te bestuderen!

Bekijk onderstaand plaatje en bedenk ook waarom onderstaande goniometrische formules gelden: (Met die formules kan je al je vragen oplossen)

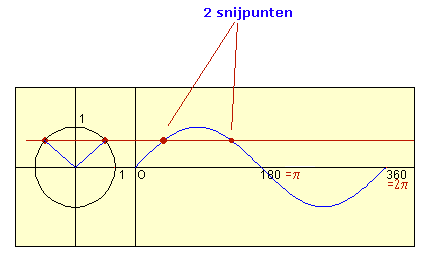
sin(a)=sin (2p+a)
sin(-a)=-sin(a)
sin(a)=sin(p-a)


Jouw vraag, "Waar blijven die 2,3 en 7?)"
Doordat de grafiek van sin(x) periodiek is met periode 2p is sin(7p/4)weer hetzelfde als sin (-p/4)=-sin(p/4).


SUcces!

ldr
maandag 17 september 2007

©2001-2024 WisFaq