Re: Goniometrische vergelijkingen, limieten en absolute waardes

Dit is een reactie op vraag 51428

Allereerst, bedankt voor de reactie!
Ik wilde toch nog even terugkomen op een vergelijking met absolute waardes, omdat het nog niet 100% duidelijk is.

Stel ik heb de volgende som:

Bereken de oplossingen x $\in$ $\mathbf{R}$ welke voldoen aan:
|x-2|·x+2·|x|-3=0

1) x = positief als x $\geq$ 2
2) x = negatief als x $\leq$ 2

1)
(-x-2)·x+2·(-x)-3=0
$\to$
-x²-2x-2x-3=0
$\to$
-x²-4x-3=0

Oplossen door of de abcformule of ontbinden in factoren.

2)
(+x-2)·x+2·(x)-3=0
$\to$
x²-2x+2x-3=0
$\to$
x²-3=0
$\to$
x²=3
x = √3

Voor het laatste vraagstukje mbt. het vinden van de nulpunten van:

x₃-2x₂-5x+6

Levert dan dus: (x-1)(x+2)(x-3)
Als nulpunten: 1, -2 en 3

Sebast
Student hbo - vrijdag 22 juni 2007

Antwoord

Dat met die absolute waarde heb je toch nog niet helemaal door. Voor x$\geq$2, vervang je |x-2| door (-x-2). Dat kan natuurlijk nooit. Ofwel verandert alles van teken, dus -x+2 (dit is voor x $<$ 2), ofwel verandert niets, dus x-2 (dit is voor x$\geq$2).

Onthoud goed de definitie, de absolute waarde van een uitdrukking in x, deze noem ik even f(x), is als volgt gedefinieerd:



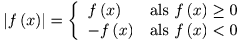
In de opgave die jij geeft, wordt het nog iets moeilijker. Je zit hier namelijk met |x-2| en met |x|, dus je gaat drie in plaats van twee gevallen krijgen. Namelijk:

Geval 1: 2$\leq$x $\Rightarrow$ |x-2| = x-2 en |x| = x
Geval 2: 0$\leq$x<2 $\Rightarrow$ |x-2| = -x+2 en |x| = x
Geval 3: x<0 $\Rightarrow$ |x-2| = -x+2 en |x| = -x

Voor die vergelijking: de ontbinding en de nulpunten kloppen.

mvg,
Tom

zaterdag 23 juni 2007

©2001-2024 WisFaq