Bewijs van Einstein voor stelling van Pythagoras

Hallo ik ben op zoek naar een bewijs voor de stelling van Pythagoras. Ik heb al vele bewijzen de revu zien passeren, maar ik ben specifiek op zoek naar een bewijs dat Einstein gemaakt heeft. Ik weet dat dit bewijs te maken heeft met gelijkvormigheid, maar meer weet ik er niet van.

Ann Ve
Student Hoger Onderwijs België - donderdag 31 oktober 2002

Antwoord

Er is inderdaad een bewijs van de Stelling van Pythagoras, dat (volgens Peter Baptist in "Pythagoras und kein Ende", 1997) afkomstig schijnt te zijn van Einstein. 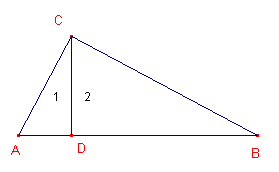Het bewijs verloopt als volgt.

Driehoek ABC is rechthoekig in C.
CD is de loodlijn op de schuine zijde.
De driehoeken ACD, CDB en ABC zijn dan gelijkvormig.
Er is een stelling die zegt, dat de oppervlaktes van gelijkvormige driehoeken zich verhouden als de kwadraten van overeenkomstige zijden.
Dus Opp(ACD):Opp(CDB):Opp(ABC) = b² : a² : c².
Zodat
Opp(ACD) =m.b², Opp(CDB) = m.a², Opp(ABC) = m.c².
We vinden dan eenvoudig: a² + b² = c².

Tja, maar eerst moet je zelf die gebruikte stelling maar bewijzen (vind ik).

Naar geschreven (Baptist) heeft Einstein het bewijs bedacht op 11-jarige leeftijd. Echter (volgens Bruno Ernst in "De interessantste bewijzen voor de stelling van Pythagoras", Epsilon), ook Naber (1908) en Bezout (1768) geven varianten van het bewijs, die erg veel op die van Einstein lijken.

Overigens, in de Elementen van Euclides staat in Boek VI, Propositie 31, een bewijs van een stelling (uitbreiding van de stelling van Pythagoras) dat van dezelfde hulpstelling gebruik maakt. Zie voor dit laatste onderstaande link.

Zie Proclus en Pythagoras

donderdag 31 oktober 2002

©2001-2024 WisFaq