Horizontale asymptoot

ik ben zelf een beetje aan het ophalen wat een horizontale asymptoot nou precies is. Ik ben er achter gekomen wat het is, en dat je een x moet laten naderen tot een heel groot getal. Verder heb ik het voorbeeld gelezen op Limiet uitrekenen.
Dit begreep ik, maar zouden jullie nog zo'n voorbeeld kunnen laten zien?
En klopt het verder dat inverse functies altijd gespiegeld zijn in de lijn y=x?

Alvast bedankt!

gea
Leerling bovenbouw havo-vwo - zondag 13 mei 2007

Antwoord

Een horizontale asymptoot is is een horizontale lijn waar de grafiek van de functie willekeurig dicht toe nadert bij grote waarden van x.
Het betreft dus altijd het gedrag van de grafiek voor x®¥ of x®-¥.
Een voorbeeldje is de grafiek van f(x)=(x²+1)/(x+1)



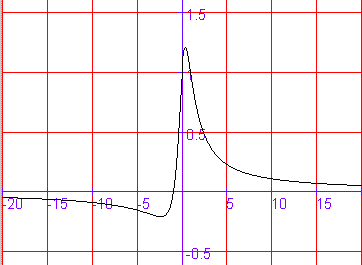
Asymptoot is hier de lijn y=0 (ofwel de x-as). Sommige mensen denken dat een grafiek de asymptoot niet kan snijden. Dat kan dus wel.
Met wat moeite kan je zelfs grafieken van functies maken die voor x®¥ en x®-¥ verschillende asymptoten hebben. Meer over asymptoten vind je bij de onderstaande link.

En klopt het verder dat inverse functies altijd gespiegeld zijn in de lijn y=x?...... Ja dus !!

Met vriendelijke groet
JaDeX

Zie Asymptoten

woensdag 16 mei 2007

©2001-2024 WisFaq