Garagedeur

Een garagedeur bestaat uit twee delen die met een scharnier aan elkaar zitten. Een van de delen zit net als een gewone deur scharnierend bevestigd aan een post. Het andere deel loopt met wieltjes in een rail langs de grond en een rail langs het plafond. Op een winternacht heeft het behoorlijk gesneeuwd. Bij het openen van de deur wordt de sneeuw weggeschoven. Met welke functie kun je de grenslijn beschrijven?

Eerst een situatieschets (in zoverre dat met de computer lukt...)levert het volgende:

       ------*          ------*---*
             \       *             /
      ------*          ------*

Het linker plaatje geeft de deur half geopend. Het rechter plaatje heeft de deur geheel geopend.
Ik noem de breedte van de deur 2a, dat betekent dat 1 deurdeel a lang is. Bij het openen ontstaan dus steeds driehoekjes met de twee korte zijdes beide lengte a en de lange zijden steeds onder elkaar en korter wordend.Als je de hoekpunten met elkaar verbindt ontstaat er uiteindelijk een kromme die wat op een S-bocht lijkt - het laatste stuk is een kwart cirkel het eerste stuk een soort omgeklapte cirkel. (Sorry, maar het lukt me niet om dat op de computer in een plaatje te zetten...).
Nu moet ik dus een formule bedenken die deze kromme beschrijft; hij lijkt op een S-bocht, ik herken een golf van een goniometriche formule of juist een derde-graads vergelijking, maar ik weet werkelijk niet hoe ik dit nu verder moet aanpakken. Enig advies is ergggg welkom.

Donald
Iets anders - dinsdag 29 oktober 2002

Antwoord

Hoi,

Dit is een verrassend moeilijke...



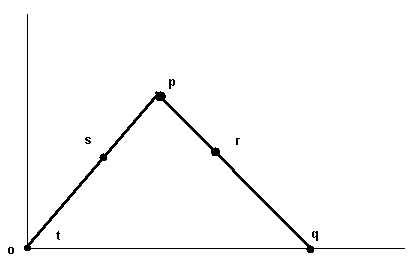
In het plaatje stellen we de poort voor en benoemen we een aantal punten. We hebben als coördinaten p(a.cos(t),a.sin(t)) en q(2a.cos(t),0).
We nemen $\mu$=0s/op en $\lambda$=pr/pq. Elk punt op het eerste stuk van de poort kunnen we dan voorstellen met s($\mu$a.cos(t),$\mu$a.sin(t)). Elk punt op het tweede door r=p+$\lambda$(q-p) of r((1+$\lambda$)a.cos(t),(1-$\lambda$)a.sin(t)). Met $\lambda$ en $\mu$ binnen [0,1].

Voor elke positie x moeten we nu bepalen:
1. Of er een punt s langskomt en zoja, welke de hoogste y-waarde y₁ is
2. Of er een punt r langskomt en zoja, welke de hoogste y-waarde y₂ is
3. het maximum y van y₁ en y₂
Deze y-waarde bepaalt de sneeuwgrens. (Als y₁ of y₂ niet gedefinieerd is, dan nemen we 0 als waarde)

Voor s zien we intuïtief dat dit voor $\mu$=1 zal zijn. Inderdaad, voor elk punt s hebben we: y=sqrt($\mu$²a²-x²) en voor vaste x dit is een strikt stijgende functie in $\mu$. Het maximum is voor de maximale waarde van $\mu$, namelijk 1. Dus: y₁=sqrt(a²-x²) (1).

Voor r is het leuker. We zien dat
(x/(1+$\lambda$))²+(y/(1-$\lambda$))²=a². Hieruit vinden we: y=(1-$\lambda$).sqrt(a²-(x/(1+$\lambda$))²) (2).
Je rekent na dat $\partial$y/$\partial$$\lambda$=0 voor $\lambda$=(2.x²/a²)^1/3-1. Je rekent ook na dat de bereikte waarde minstens zo groot is als voor $\lambda$=0 of $\lambda$=1, en dat we inderdaad een maximum bereiken.
Met deze waarde in (2) vinden we een uitdrukking van y₂ in functie van x.

Nu moet ik toegeven dat ik het niet nagerekend heb, maar vermoedelijk is y₂>=y₁ voor x in [0,a]. Grafisch (a=5) blijkt dit in ieder geval te kloppen. Intuïtief/meetkundig lijkt het aannemelijk, maar niet evident... Toch even narekenen als je tijd hebt.



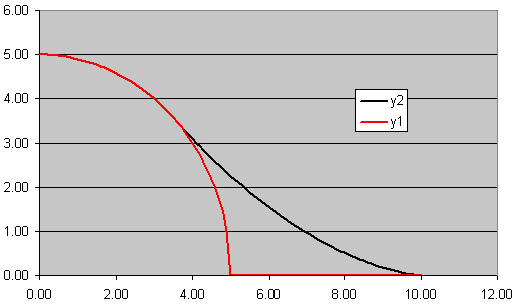
De vergelijking is dus:
y=(1-$\lambda$).sqrt(a²-(x/(1+$\lambda$))²)
met $\lambda$=(2.x²/a²)^1/3-1. Misschien kan je dit nog wat vereenvoudigen, maar dit laat ik aan jou...

Groetjes,
Johan

andros
dinsdag 29 oktober 2002

©2001-2024 WisFaq