Kortste wegen

Hallo,

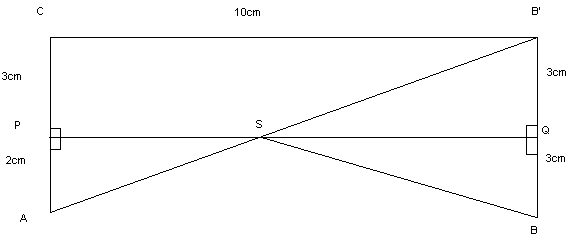
ik heb de volgende vraag: bereken in drie decimalen nauwkeurig de lengte van de weg van A naar B via S.



En ik had het opgelost op twee manieren, maar die blijken verschillende antwoorden te geven.

Manier 1: PAS gelijkvormig met SBQ = 2/3

√(2²+(¹/₃ x 10)²) + √ (3²+(²/₃ x 10)²) = 11,20

Manier 2: CA² + CB'² = AB'²
√(10²+5²) = 11,18

Nu is mijn vraag, wat doe ik fout en waarom is het niet gelijk?

Bedankt voor het uitleggen!

Tsunki
Leerling bovenbouw havo-vwo - zondag 11 maart 2007

Antwoord

Als S het punt is dat hoort bij de kortste route dan verdeelt S het lijnstuk PQ niet in de verhouding 1:2 maar in de verhouding 2:3. Als je dat niet 'meteen' ziet dan is dat te berekenen met:



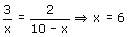
Op de eerste manier krijg je dan:



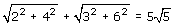
Op de tweede manier:



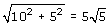
En dan klopt het allemaal!

zondag 11 maart 2007

©2001-2024 WisFaq