Rationale functies

Ik zit met een probleem, weer een, wanneer moet je eigenlijk een euclidische deling gebruiken in rationale functies?

lori
3de graad ASO - woensdag 16 oktober 2002

Antwoord

Bij rationale functies (laten we zeggen dan dit functies zijn die bestaan uit een quotiënt van veeltermen) kan je m.b.v. limieten bepalen of de grafiek horizontale en verticale asymptoten heeft. Om te bepalen of de functie een schuine asymptoot heeft, kan je de 'euclidische deling' gebruiken.

Op Euclidisch delingsalgoritme voor veeltermen bijvoorbeeld staat een voorbeeld van zo'n deling.
Het blijkt dat je de functie:



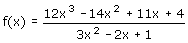
kan schrijven als:



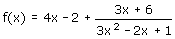
..en hieruit kan je een belangrijke conclusie trekken. Als x®¥ dan gaat de laatste 'breuk' naar nul. Dat betekent dat de grafiek bij x®¥ steeds meer op g(x)=4x-2 gaat lijken. De grafiek van f heeft dus als schuine asymptoot de lijn y=4x-2.

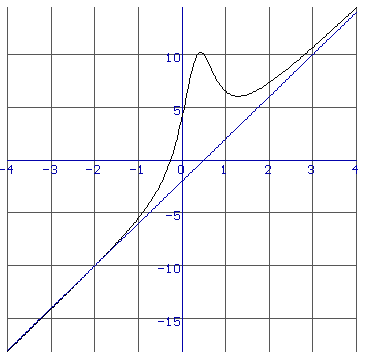
woensdag 16 oktober 2002

©2001-2024 WisFaq