Wat is de formule voor de hoek tussen twee snijdende grafieken?

bereken de hoeken waaronder de grafieken van f en g elkaar snijden in o en b

beide grafieken zijn geen rechten, bovendien zijn de coordinaten van o en b gekend, weet u hier een formule voor?

Nathan
3de graad ASO - zaterdag 4 november 2006

Antwoord

Allereerst: de hoek die twee snijdende krommen met elkaar maken, is gelijk aan de hoek die de bijbehorende **raaklijnen** in dat punt met elkaar maken. (ga maar na).
Van die raaklijnen en hun eigenschappen, zullen we t dus moeten hebben.

als je de coördinaten van het snijpunt hebt. En je hebt de functievoorschriften van f en g, dan ben je al een heel eind. ;-)

Wanneer je immers de x-coördinaat invult in de afgeleide van f (of g) dan levert dat de tangens op van de hoek die de RAAKLIJN maakt aan f (of g) in dat punt, met de horizontale as.

noem de tangens van de hoek die de raaklijn aan f maakt met de x-as: tana; En noem de tangens van de hoek die de raaklijn aan g maakt met de x-as: tanb.

je kunt dan gebruik maken van de formule

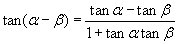
om aan de gevraagde hoek te komen.
Deze formule volgt uit tanx = sinx/cosx, en
sin(a-b) = sinacosb - cosasinb,
cos(a-b) = cosacosb + sinasinb

groeten,
martijn

mg
zondag 5 november 2006

©2001-2024 WisFaq