Zwaartepunt van een omwentelingslichaam

Hey,

Ik kom echt niet uit deze vraag:

Je hebt een omwentelingslichaam dat ontstaat door de grafiek van f(x)= x² met domein [0,1] om de x-as te wentelen. Bereken de plaats van het zwaartepunt van dit omwentelingslichaam.

Kunnen jullie me dit aub stapsgewijs uitleggen? Ik heb hier erg moeite mee

Mark H
Leerling bovenbouw havo-vwo - maandag 16 oktober 2006

Antwoord

Beste Mark,
dan zullen we het probleem van het zwaartepunt stapsgewijs opbouwen, van simpel naar iets ingewikkelder.
zwaartepunt. eerst simpel uitgelegd:
Stel je hebt 2 (punt-)massa's m₁ en m₂, en deze bevinden zich op een afstand s van elkaar. Waar ligt het zwaartepunt?



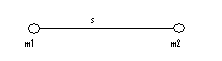
In zo'n geval moet je wel eerst een coördinatenstelsel kiezen. Het handigst is een coördinatenstelsel met de oorsprong in 1 van de puntmassa's:



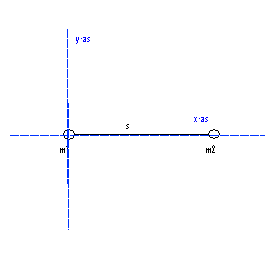
De formule voor het zwaartepunt is z= m₁x₁+m₂x₂/(m₁+m₂)
(in dit voorbeeld is x₁=0)

Als er nu niet 2 maar meerdere massa's zijn die zich op 1 lijn bevinden (bijv. n massa's), dan luidt de formule voor het zwaartepunt:
z=m₁x₁+m₂x₂+...+m_nx_n/(m₁+m₂+...+m_n)



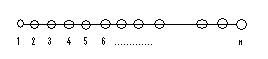
De voorbeelden gingen tot dusver over 1 dimensie. Wanneer er n (punt)massa's verdeeld zijn over de ruimte, dus in 3 dimensies, dan moet het zwaartepunt ook in 3 coördinaten worden uitgedrukt, de x, de y en de z-coördinaat. De formule luidt dan:
z=m₁x₁+m₂x₂+...+m_nx_n/(m₁+m₂+...+m_n)

Nu jouw omwentelingslichaam:
Dat kunnen we voorstellen als oneindig veel 'plakjes' met dikte dx, oppervlakte $\pi$y², en afstand x tot de oorsprong:



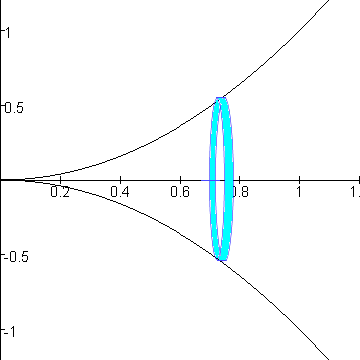
Stel eens dat het omwentelingslichaam overal dezelfde dichtheid $\rho$ heeft.
De massa van het plakje is gelijk aan het volume maar de dichtheid,
dus m = V.$\rho$ = A.dx.$\rho$ = $\pi$.y².dx.$\rho$

In feite zijn er oneindig veel plakjes,... met oneindig kleine massa dm. en elk plakje bevindt zich op afstand x van de oorsprong.
Omdat het een omwentelingslichaam is, bevindt het zwaartepunt zich op de x-as. Het object is namelijk symmetrisch om de x-as.
Voor het zwaartepunt geldt dan:
z=$\int{}$x.dm / $\int{}$dm
= $\int{}$x.$\pi$.y².dx.$\rho$ / $\int{}$$\pi$.y².dx.$\rho$
($\pi$ en $\rho$ zijn constanten die tegen elkaar wegvallen in teller en noemer)
= $\int{}$x.y².dx / $\int{}$y².dx
= $\int{}$x.(x²)²dx / $\int{}$x⁵dx / $\int{}$x⁴dx
= [1/6.x⁶]/[1/5.x⁵]
(grenzen van 0 tot 1)
= (1/6)/(1/5)
= 5/6

groeten,
martijn

mg
dinsdag 17 oktober 2006

©2001-2024 WisFaq