Scalair product

Ik ben momenteel bezig met een herhalingscursus wiskunde.

Ik vond in het onderdeel volgende terug:

e(alpha) en e(beta) zijn beiden beeldpunten van een hoek op de goniometrische cirkel.

De x-as wordt weergegeven met de vector e(0) en de y-as met de vector e(teta).

Als we nu logisch gaan redeneren in de goniometrische cirkel kunnen we met behulp van pytahoras volgende stelling afleiden:

vector e(alpha) = cos (alpha) . vector e(0) + sin (alpha) . vector e (teta)

(Hetzelfde is trouwens ook mogelijk voor beta)

Dit kan ik perfect op de goniometrische cirkel afleiden.
Nu probeert men hier echter de grondformule van de goniometrie uit af te leiden. Dit door vector e (alpha) te kwadrateren op twee manieren:

( vector e (alpha) )² = 1 = Hoe komen ze hieraan? Mag je de waarde 1 toekennen omdat we in de standaard gonio cirkel werken?

EN

( vector e (alpha) )² = (cos (alpha) . vector e(0) + sin (alpha) . vector e (teta))
²

= (cos (alpha) . vector e(0))² + 2 cos(alpha) sin (alpha) vector e(0) vector e (teta) + (sin (alpha) . vector e (teta))² = Dit is gewoon het dubbel product uitwerken

= cos (alpha)² + sin (alpha)² Uit de vorige stap haalt men dus dit. Hoe komt men hieraan?

Nu kunnen we natuurlijk deze gelijk stellen aan elkaar en hebben we de grondformule. Als iemand even een beetje moeite wil doen om deze twee stappen te verklaren? Alvast dank.

Pieter

Pieter
Student Hoger Onderwijs België - dinsdag 22 augustus 2006

Antwoord

Waarschijnlijk ken je wel de stelling van Pythagoras: Die zegt dat het kwadraat van de lengte van de schuine zijde in een rechthoekige driehoek gelijk is aan de som van de kwadraten van de lengtes van de rechthoekszijden.
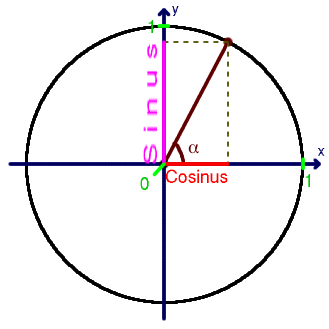
Bekijk even onderstaande figuur. Beschouw de rechthoekige driehoek met de rode rechthoekszijde, de stippelrechthoekszijde, en de donkerrode schuine zijde.
dan zegt Pythagoras:
(rode rechtoekszijde)²+(stippelrechthoekszijde)² = (donkerrode schuine zijde)²

Maar de rode zijde is de cosinus, de stippelzijde is evenlang als de roze zijde en is dus de cosinus, en de donkerrode schuine zijde is de straal van de goniometrische cirkel en is dus 1
er komt dan vanzelf:
cos²+sin²=1



Als je deze stap in jouw berekeningen bekijkt:

(cos (alpha) . vector e(0))² + 2 cos(alpha) sin (alpha) vector e(0) vector e (teta) + (sin (alpha) . vector e (teta))))²

De eerste term is cos(alpha)² want de lengte van vector e(0) is 1 (straal van de goniometrische cirkel)
idem voor de laatste term met de sinus.

De middelste term is nul aangezien vector e(theta) en vector e(0) loodrecht staan (inproduct van loodrechte vectoren is nul)

vrijdag 25 augustus 2006

©2001-2024 WisFaq