Binomiale verdeling

Hai ik heb de volgende 2 vragen:

X:het aantal keer een 5 bij 600 worpen met een zuivere dobbelsteen
a. bereken P(100$<$X$<$104)
b. bereken k zó dat P(X$\geq$k)$<$0.05

Ik snap bij allebei van deze niet hoe ik bij de eerste X en bij de tweede k moet berekenen...
Alvast bedankt!

Alexan
Leerling bovenbouw havo-vwo - dinsdag 30 mei 2006

Antwoord

a.
Je kan de kans berekenen met de binomiale verdeling.
X:aantal keren 5 gooien
n=600
p=¹/₆
X~Bin(600,¹/₆)
Gevraagd: P(100$<$X$<$104)

P(100$<$X$<$104)=P(X$\leq$103)-P(X$\leq$100)
...of...



Nu zou moeten gelden: 0.6531 - 0.5267 = 0.1264
Klopt!

Uiteraard kan je de kans ook benaderen met de normale verdeling.
Zie Binomiaal en benadering met de normaal verdeling voor een voorbeeld. Denk aan de continuiteitscorrectie!

b.
Dit is iets lastiger..., maar met je GR gaat het wel. Ik maak gewoon een tabel... Stel dat de vraag was

• Bereken k zodat P(X$\leq$k)$\leq$0,05

Dat kan dan bijvoorbeeld op de volgende manier:







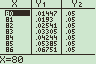
Conclusie? k=84
Nu jij weer... maar dan voor P(X$\geq$k)<0,05

P.S.
Als je niet 'weet' dat je zo rond de 80 moet beginnen (en waarom zou je dat weten?) kan je natuurlijk eerst met 0 beginnen in stappen van 10... en dan 's kijken en dan verder 'inzoomen', tabelgewijs dan...

Uiteraard kan je hier ook weer de benaderen met de normale verdeling en dan kan je natuurlijk wel terugrekenen... Dat kan natuurlijk ook. Denk aan de continuiteitscorrectie! Een interessante vraag is nu: moet je hier de normale verdeling gebruiken of niet?

woensdag 31 mei 2006

©2001-2024 WisFaq