Wig van Wallis

wij hebben de volgende formule gevonden voor het bepalen van het zwaartepunt van de wig van Wallis :




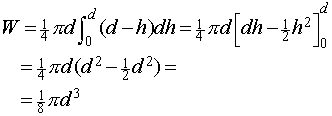
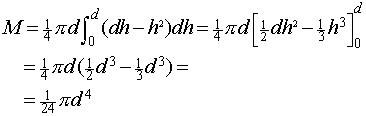
Voor het zwaartepunt Z van de wig, dat gelegen is op de z-as, hebben we dan:
W.z = M
waaruit volgt dat z = 1/3d

Zou iemand mij kunnen uitleggen hoe ze aan deze formule zijn gekomen?

Zie http://www.pandd.demon.nl/rhino/wig_wallis2.htm

Lars v
Leerling bovenbouw havo-vwo - woensdag 3 mei 2006

Antwoord

Je kunt de wig zien als een stapel heel dunne ellipsvormige plakken; op hoogte h is de lange as gelijk aan d en de korte as gelijk aan d-h; de oppervlakte van zo'n ellips is dus pi*d*(d-h)/4. De totale inhoud krijg je dat dor die formule te integreren van 0 tot d.
Elk ellipsje heeft als moment kracht maal arm en dat is dus pi*d*(d-h)/4 maal h; door dat te integreren krijg je het moment in de z-richting. De z-coordinaat van het zwaartepunt is het quotient van moment en massa.

kphart
woensdag 3 mei 2006

©2001-2024 WisFaq