In lissajousfiguren de t berekenen

hallo, ik ben mijn huiswerk aan het maken maar kom niet uit de volgende opgave:


gegeven:
de kromme K: (pv) x=cos t en y=cos3t met op [0,p]

de vraag:
Bij K hoort een formule van de vorm y=ax^(3)+bx
geef a en b en toon aan dat de formule juist is.

Het aantonen dat zal me waarschijnlijk wel lukken, maar ik begrijp niet hoe je uit die figuur (als ik die geplot heb in mijn GR) de vorm y=ax^(3)+bx kunt afleiden.

Alvast bedankt!!!

grtjs anne

anne
Leerling bovenbouw havo-vwo - donderdag 20 april 2006

Antwoord

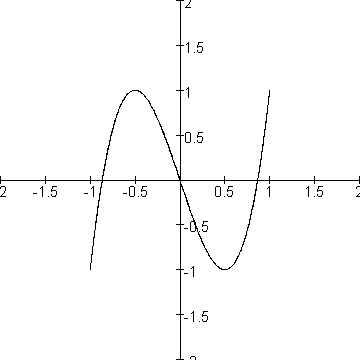
Als ik in het plaatje kijk lijkt de figuur te gaan door het punt (1,1)
Even controleren: kies t=0, dan krijg je het punt (cos(0),cos(0))=(1,1) klopt.
x=1 en y=1 invullen in y=ax³+bx levert 1=a+b.
De kromme lijkt ook te gaan door de punten (0,0) en (-1,-1) maar dat levert niet zoveel nieuws op: (0,0) invullen in y=ax³+bx levert 0=0. (-1,-1) invullen levert -1=-a-b en dat is hetzelfde als 1=a+b.
We zullen nog een derde punt nodig hebben.
Kiezen we t=¹/₃p dan krijgen we (cos(¹/₃p),cos(p)=(¹/₂,-1)
Vullen we dit in in y=ax³+bx dan krijgen we -1=¹/₈a+¹/₂b
Vermenigvuldigen we de laatste vergelijking met 8 dan krijgen we -8=a+4b, dus a=-8-4b.
Vullen we dit in in a+b=1 dan krijgen we -8-4b+b=1, dus -3b=9, b=-3
Dit invullen in a+b=1 levert a=4.
Voor dat aantonen dat de formule inderdaad juist is moet je cos(3t) uitdrukken in cos(t).
Je kunt dit doen door cos(3t) te schrijven als cos(2t+t) en de som en verdubbelingsformules te gebruiken.

donderdag 20 april 2006

©2001-2024 WisFaq