2de graads 2onbekenden

Ik heb de vergelijking

k² + 10k = d²+ 34d +5

Voor de oplossing van het probleem maakt het waarschijnlijk niet uit, maar het kan helpen:
domeinen in dit voorbeeld zijn
voor k: {1...25}
voor d: {1...8}

volgens jullie link naar WINS (http://www.wisfaq.nl/showrecord3.asp?id=22342)
is dit te herschrijven als

k=+/- √(d²+34d+25-5)
en
d=+/- √(k²+10k+25-5)

en dat zal wel kloppen, alhoewel...als ik daarbij de abc-formule gebruik bij k dan slaan die waardes (√(33.4) of √(0.59..) nergens op.

Bij d zou de oplossing niet eens mogelijk zijn omdat 4ac groter is dan b².

Kortom, de vraag is: welke methode of welke theorie kan ik voor het vinden van de juiste d en k hierbij het beste gebruiken?

(zonder alle mogelijkheden in de domeinen te proberen)
De oplossing is d=5 en k=10.

Alvast bedankt voor jullie aandacht.
David

David
Iets anders - zaterdag 1 april 2006

Antwoord

De relatie k² + 10k = d²+ 34d +5 legt een verband vast tussen d en k. Zonder verdere voorwaarden zijn er een oneindig aantal combinaties van d en k die hieraan voldoen.
De formules die je bij WIMS hebt gevonden geven aan hoe je d kunt berekenen als je k hebt en omgekeerd. Overigens heb je die fout overgenomen.
Hieronder de uitdrukkingen die je hebt gekregen:


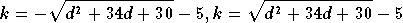
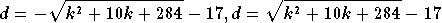
Uit je verdere vraag begrijp ik dat je gehele waarden voor d en k zoekt zodat de relatie opgaat.
Bekijken we de uitdrukking
k=±√(d²+34d+30)-5 dan moet dus gelden dat
d²+34d+30 een zuiver kwadraat is.
d=0 levert 30 en dat is geen kwadraat.
Elke keer dat we d met 1 verhogen neemt d² toe met 2d+1 en neemt 34d toe met 34,
dus
d=1 levert 30+(2·0+1)+34=65
d=2 65+(2·1+1)+34=102
d=3 102+(2·2+1)+34=141
d=4 141+(2·3+1)+34=182
d=5 182+(2·4+1)+34=225 en dit is het kwadraat van 15.
dus k is dan √(225)-5=15-5=10.

zaterdag 1 april 2006

Re: 2de graads 2onbekenden

©2001-2024 WisFaq