Harmonische reeks wat is de limit?
Hi wisfaq,
Ik zit met een dringende vraag, ik zag laatst op TV over een wetenschappelijk quiz, en dat ging over een brug bouwen met stenen die zoveel mogelijk kan helt van zijn stamplaats (meer levendiger voorbeeld toren van pizza idee) maar dan met tegels en de vraag is dan wat is ongeveer de max dat hij kan hellen opdat de toren zal omvallen. Okey er bleek een wiskundig verband te zijn..en dat werd aangegeven met
1/2 + 1/4 + 1/6 + 1/8+ ....+ 1/(2+2n)+...
Hij beweerde hierbij dat deze reeks dus oneindig is..maar dit is toch een convergerende reeks?? dus dit heeft toch een limiet. Mijn vraag is hoe bereken je het limiet waarbij n naar oneindig gaat?
Een heel verhaal maar hoop dat je begrijpt waar het over gaat.
ik heb ook nog wat op internet gevonden.
http://dutiaw37.twi.tudelft.nl/~kp/stukjes-pythagoras/jg40/juni-2/node3.html
mvg.
John
Student universiteit - maandag 26 december 2005
Antwoord
Bekijk de functie f(x)=1/x op het interval [1,p] met p geheel.
We tekenen nu rechthoekjes als in onderstaande tekening.
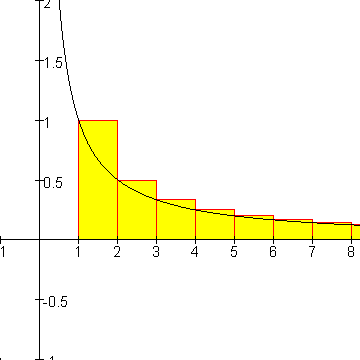
De som van de oppervlakten van de rechthoekjes is 1+1/2+1/3+1/4+....+1/p-1.
Deze som van oppervlakten is duidelijk groter dan $\int{}$1p(1/x)dx=ln(p)-ln(1)=ln(p).
Omdat limp$\to\infty$ln(p)=$\infty$ is de som van de oppervlakten van deze rechthoekjes voor p$\to\infty$ zeker $\infty$
maandag 26 december 2005
©2001-2024 WisFaq
|
Re: Harmonische reeks wat is de limit?