In te leggen bedrag bij maandelijkse annuïteiten

Ik ben bekend met de formules m.b.t. annuïteiten-spaarvormen en die m.b.t. leningen. Het lukt mij echter niet om uit te rekenen hoeveel ik maandelijks moet inleggen als ik in 15 gelijke, jaarlijkse termijnen een eindbedrag wil realiseren van bijvoorbeeld €150.000, waarbij ik:
a. eerst 10 jaar spaar tegen 6,5% rente
b. dan 5 jaar de lening voor het resterende bedrag aflos
c. ook nog eens 1,9% van de inleg (over de gehele 15 jaar) betaal voor een bijkomende premie.
Ik heb teveel variabelen! Ik zoek hiervoor de (samengestelde) formule, omdat ik ook wil weten hoe de inleg eruit ziet als ik de looptijden van a. en b. verander.
Kunt u me helpen?

Ellen
Iets anders - dinsdag 27 augustus 2002

Antwoord

Je vraag is vrij gecompliceerd en je hebt inderdaad te veel variabelen om het eenvoudig op te lossen. Ik zal de formule stapje per stapje opbouwen, zodat als ik je vraag iets verkeerd geïnterpreteerd heb, je zelf de nodige aanpassingen kunt doen. Ook ga ik er in het begin van uit dat de inleg geheel bij de aanvang gebeurt. Pas op het einde ga ik over tot mensualiteiten (maandelijkse inbreng).

a) eerste 10 jaar sparen tegen 6.5%

Formule: V_n=V₀.(1+r)ⁿ

Deze formule berekent bij een gekende aanvangswaarde V₀, een gegeven duur n (jaar) en (samengestelde) rentevoet r de slotwaarde. In dit geval met een gewenst eindbedrag van €150.000 (nu verondersteld na 10 jaar) krijg je:
€150.000 = V₀ . (1 + 0.065)¹⁰
V₀ = 79.909 inleg bij aanvang


b) b) dan 5 jaar de lening aflossen voor het resterende bedrag

Hier heb ik te weinig gegevens voor. Zoals ik het begrijp los je dan in 5 jaar tijd het bedrag van de lening af. Ik neem aan dat je de lening in jaar 1 aangaat. Dan krijg je later in de formule: 5 * bedrag lening / 5 = bedrag lening.

Je bent waarschijnlijk vergeten te vermelden dat je gedurende die 15 jaar ook intrest moet betalen: je krijgt dan de formule uit a) maar met V₀ negatief (geld dat je uitgeeft).

Tot nu toe:





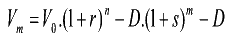
Met n = aantal jaar dat je eerst spaart
m = totale tijdsduur
r = rente sparen
s = intrest lening
Vm = eindbedrag na m-jaar
V0 = aanvangswaarde (inleg)
D = bedrag lening

Als je de gegevens van de lening kent, is ook hier de aanvangswaarde gemakkelijk uit te halen. Zoals ik het begrijp, weet je niet zo veel van de lening: gebruik dan een fictief leningbedrag om V₀ te berekenen, zodat je maar 1 onbekende hebt.

c) 1,9% van de inleg jaarlijks betalen voor een bijkomende premie

Ik ga ervan uit dat het enkel om de aanvangsinleg gaat (nu maakt dit nog geen verschil, maar wel voor de mensualiteiten, want dan heb je elke maand een inleg). Dit is dan eenvoudig op te lossen: in de vorige formule komt erbij: -V₀.(1+t)^m met t = 0,019 en m = 15

Dit geeft dan voor het te zoeken inlegbedrag:





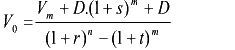
Nu kan je ook gemakkelijk het aantal jaar sparen en lening aflossen aanpassen: gewoon de waarde van exponent n aanpassen. Voor de aflossing van de lening maakt dit geen verschil: of je nu op 5 jaar of op 6 jaar aflost: je moet hetzelfde bedrag betalen.

Je bekijkt het te aflossen deel misschien eerder als het totale bedrag van de lening en de jaarlijkse intresten en hoe eerder je dan begint af te lossen, hoe minder intresten je uiteindelijk moet betalen. Dan is de volgende formule een vrij goede benadering (je betaalt de laatste jaren steeds minder intrest in de mate van de jaarlijkse gelijke afbetalingen).





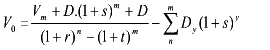
Met Dy = uitstaand bedrag van de lening in jaar y

Opmerking: je inlegbedrag zal vrij hoog zijn omdat je nog een bedrag wilt overhouden en omdat de leningaflossing reeds ingecalculeerd is. Het element sparen wordt grotendeels tenietgedaan door de lening.

TIP: in Excel is dit allemaal vrij snel te bereken. Als je de variabelen (lening, intrest, looptijd,…) in aparte cellen opneemt en in de formule verwijst naar deze cellen, kan je zelf de variabelen wijzigen en het effect onmiddellijk zien.
Formule annuïteit = TW(rate, aantal periodes, bedrag per termijn, gewenste huidige waarde, annuïteit of perpetuïteit). Enkel de drie eerste waarden zijn verplicht.

Aanpassingen:
1) jaarlijkse inleg i.p.v. alles inleggen aan het begin: In de vorige formule wijzigt Vm / noemer in:





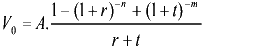
Dit laatste is een eigenschap van meetkundige rijen.

met A = jaarlijkse inleg

Aan het leninggedeelte moet niets veranderd worden

Opgelet: door de wijziging is Vm verdwenen waarin het gewenst eindbedrag staat.

2) mensualiteiten:

idem als hierboven: enkel de rente delen door 12 (maandbasis) en de exponenten vermenigvuldigen met 12. Wanneer je de lening per maand afbetaalt, doe je met het leninggedeelte hetzelfde). Je krijgt dan als uiteindelijke formule (met jaarlijkse leningaflossing):





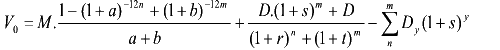
Met M = maandelijks in te leggen bedrag
a = intrest (sparen) per maand
b = rente (op inleg voor premie) per maand


Als je het resultaat wilt weten met een eindbedrag van €150.000 stel dan V₀ gelijk aan – 150.000 (in principe 0) en haal dan M eruit, zodat je het maandelijks in te leggen bedrag kent.

zondag 1 september 2002

©2001-2024 WisFaq