Metalen plaatjes en een soldeerverbinding

Ik heb twee metalen plaatjes van 1 mm dik aan elkaar gesoldeerd met een prismatische soldeerverbinding van 0.3 mm breed. de metalen plaatjes zijn veel sterker dan het soldeer en zijn dus star te veronderstellen. nu wordt dit geheel neergelegd op een houder met daarin een gat van 4 mm breed (soldeerspleet in het midden) en wordt er met een "punch" op het soldeer gedrukt, zodat (alleen het soldeer) doorbuigt. Het soldeer buigt nu door en kijgt zowel boven als onder de vorm van een cirkelboog. Ervan uitgaande dat de plaatjes op de hoekpunten vast blijven liggen weet ik de lengte van de plaatje tussen hoekpunt van de houder en soldeerspleet. Verder meet ik de verplaatsing aan de bovenzijde van de soldeerverbinding, die is dus ook bekend. Echter, doordat het soldeer er in gedeformeerde toestand uitziet als een cirkelboog met steeds kleiner wordende R (bij verder gaande deformatie) krijg ik door het toepassen van driehoeken de waarde van R (straal van de cirkelboog aan de onderzijde) niet te pakken. Is er een manier waarop dit is uit te rekenen ?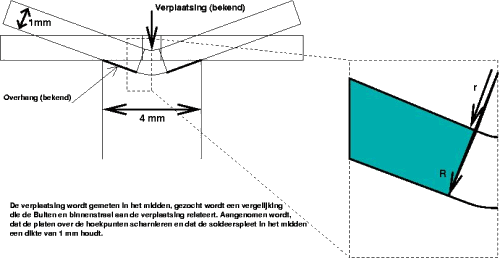

Groeten

Jeroen
Student universiteit - woensdag 7 augustus 2002

Antwoord

Hoi Jeroen!

Met driehoeken kwam ik er ook niet uit, en met enkel de verplaatsing ook niet. Als je echter weet onder welke hoek de plaatjes verdraaid zijn, dan kun je uitrekenen wat de verplaatsing was.

Je weet dat als je de raakvlakken plaatje/soldeer doortrekt, dat die samenkomen in het middelpunt van de cirkel.





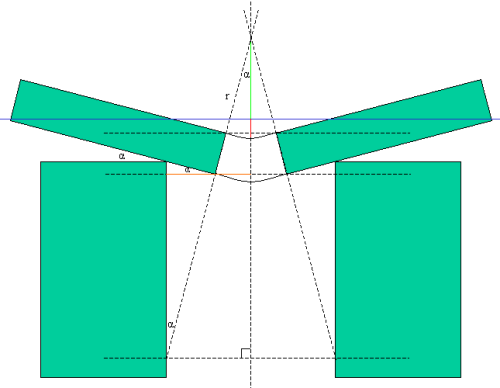
Je kunt dan vanuit het middelpunt van de cirkel een gelijkbenige driehoek construeren die langs het vlak plaatje/soldeer loopt. Je weet dat de basis van die driehoek 4mm is. Het rode lijnstuk is de verplaatsing, dus de straal minus het groene lijnstuk geeft de verplaatsing. De blauwe lijn geeft het niveau aan waar de plaatjes lagen voor de verbuiging.

Noem de halve tophoek van die driehoek a. Op basis van gelijkvormigheid zijn dan nog wat hoeken ook a.

Neem nu het oranje lijnstuk. Dit lijnstuk wordt in 2-en verdeeld door het hoekpunt van het plaatje. Je weet dat het 2mm lang is (de helft van de opening). Je weet ook dat het overstekende deel van het plaatje 1,85mm is, nl. (4 - 0,3) / 2.

Stel nu dat a = 5 graden.

Je kunt nu uitrekenen dat het linkergedeelte van het oranje lijnstuk cos(5)·1,85 = 1,843mm is . Het rechtergedeelte is dan 2 - 1,843 = 0,157 mm.

De straal van de buitenste cirkel is dan 0,157 / sin(5) = 1,802mm. De binnenste cirkel is dan 1mm kleiner, dus r = 0,802mm.

Dan de verplaatsing. De loodlijn vanuit het middelpunt van de cirkel op het oranje lijnstuk is (1,802² - 0,157²) = 1,795mm.

De afstand tussen het oranje en het blauwe lijnstuk is sin(5)·1,85 + 1 = 1,161mm. Het groene lijnstuk is dan 1,795 - 1,161 = 0,634mm.

De verplaatsing is dan 0,802 (r) - 0,634 = 0,168mm.

Op deze manier kun je een tabelletje construeren voor een aantal a's, en daaruit kun je dan de straal bij een bepaalde verplaatsing aflezen. Het is me niet gelukt om die twee rechtstreeks te relateren.

mschapen
vrijdag 9 augustus 2002

©2001-2024 WisFaq