Re: Algebraïsche bewijsvoering van de driehoek van Pascal
Is er een mogelijkheid iets duidelijker te zijn? Sites heb ik ook in overvloed gevonden.... en vooral Engelse... Maar daar snap ik dus totaal niks van... Bovendien kan ik niet zeggen dat ik over een wiskundeknobbel beschik... Anders had ik hier mijn vraag toch ook niet gesteld?
Stan
Leerling bovenbouw havo-vwo - dinsdag 31 mei 2005
Antwoord
Dat laatste is onzin! Er zijn ook echte bollebozen die hier vragen stellen! Maar je kan niet alles hebben, dus zullen we een voorbeeld doen!
Je zoekt op de website een leuke stelling op:
Bijvoorbeeld deze:
In de driehoek van Pascal geldt:
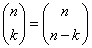
Vervolgens kijk je bij het bewijs en gaat na of je dat kan volgen:
We weten:
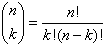
en
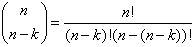
Kan je nu laten zien dat daar twee keer hetzelfde staat?
Ja hoor best wel!
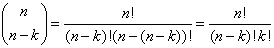
Er geldt immers (n-(n-k))=k
Als je nu iets over de driehoeksgetallen in de driehoek van Pascal wilt bewijzen dan klik je op http://binomial.csuhayward.edu/Identities.html#Tri2Row2
Er staat:
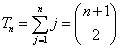
Known as: The relationship between the triangular numbers Tn and the 2nd column of Pascal’s Triangle.
Maar nu het bewijs...!? (dat staat er niet bij...)
In WisFaq kan je vrij makkelijk vinden dat:
Tn = n · (n+1) / 2
Zie Driehoeksgetallen.
Nu zou je moeten laten zien dat hetzelfde is als  .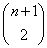
En dat kan zo:
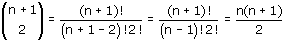
Die laatste stap moet je dan maar 's zelf uitzoeken, maar och je mag zelf natuurlijk ook wel IETS doen...
En voor de rest toch maar 's op de website kijken...
Zie Binomial Coefficient Identities and Proofs Listed by Category
dinsdag 31 mei 2005
©2001-2024 WisFaq
|
Dit is een reactie op vraag 38759