Stellingen bewijzen

Ik heb wel het antwoord van hoe je van een rechthoek een vierkant maakt met dezelfde oppervlakte, maar waarom is dat zo? Hoe bewijs je dat het klopt?
(in euclides elementen staat niets!!!)

Lida G
Leerling mbo - maandag 17 juni 2002

Antwoord

Uitgaande van de constructie van vraag 136 (zie ikoontje hiernaast) krijg je deze figuur:



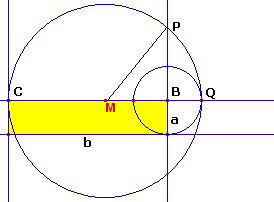
Je ziet hier een rechthoek met zijde a en b. De oppervlakte van de rechthoek is dan a·b. We moeten nu bewijzen dat BP (de zijde van her vierkant met dezelfde oppervlakte) de lengte heeft (ab).

In de constructie is BQ gelijk aan a. Je zoekt het midden M van CQ. De cirkel met middelpunt M heeft als straal (a+b)/2.
MP=(a+b)/2=½a+½b
BM=MQ-a=½a+½b-a=-½a+½b
In driehoek MBP geldt de stelling van pythagoras. Dus
BP²=(½a+½b)²-(-½a+½b)²=ab (controleren!)
Dus BP=(ab)

Waarmee de constructie bewezen is.

maandag 17 juni 2002

©2001-2024 WisFaq