Vergelijking van een vlak door punt P, dat een rechte a bevat

zoek de cartesiaanse vergelijking van een vlak alfa door punt P(2,1,-1). Je weet ook: vlak alfa omvat de rechte
a$\leftrightarrow$ ¹/₄ (x+2)= -¹/₂ (y+3)= z+1

ik heb nog een oefening die niet lukt:
Bepaal de cartesiaanse vergelijking van alfa door rechten a en b.
a$\leftrightarrow$ x+y+z=2
$\leftrightarrow$ 2x-y=3
b$\leftrightarrow$ 2x+y+z=3
$\leftrightarrow$ 3x+2y+z=3

Alvast bedankt

Stefan
3de graad ASO - dinsdag 15 maart 2005

Antwoord

Beste Stefanie,

Er is al één punt gegeven en uit de vergelijking van die rechte kan je nog een punt halen en ook een richting.
Met die twee punten en de richting kan je dan de vergelijking van het vlak bepalen.

Als je de rechte dan schrijft in de standaardvorm kun je deze gegevens rechtstreeks aflezen, (x₀,y₀,z₀) is dan een punt van de rechte en (a,b,c) een stel richtingsgetallen.



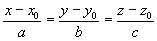
In jouw geval dus:



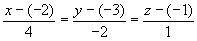
Met als punt (-2,-3,-1) en richting (4,-2,1).
Het extra gegeven punt was (2,1,-1).

Vul nu een 4x4 determinant met de onbekenden x,y,z in de eerste rij (met een "1" erachter), rijen met punten krijgen ook een "1" erachter en richtingen een "0". Stel deze determinant gelijk aan 0 en werk uit door te ontwikkelen naar de eerste rij: je krijgt dan de vergelijking van het vlak:



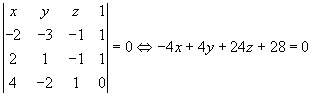
Deze methode met een determinant om de vergelijking van een vlak op te stellen kan je ook gebruiken voor je 2e probleem. Zoek bijvoorbeeld een punt op elke rechte en een richting, of 3 (niet collineaire) punten op die rechten en pas bovenstaande methode toe.

mvg,
Tom

dinsdag 15 maart 2005

©2001-2024 WisFaq