Vraagstuk met exponentiele vergelijkingen

Hoi wisfaq
Zouden jullie me kunnen helpen met de volgende opgave?

Op het ogenblik t=0 wordt een voorwerp met temperatuur T0 °C in een omgeving met temperatuur M °C gebracht (T0 M). Na een tijdsverloop van t h bedraagt de temperatuur van het voorwerp nog T °C. Volgens een wet van Newton geldt:
t=1/k*ln((T0 - M)/(T-M))
Hierin is k een consante waarvan de waarde eigen is aan het voorwerp.
In een kamer waarvan de temperatuur onveranderd op 18°C blijft, wordt het slachtoffer van een moord gevonden, precies om 8u35. De detectieve die belast is met het onderzoek, constateert op dat ogenblik dat de temperatuur van het lichaal nog 32°C bedraagt. Een uur later is de temperatuur 29°C. Ga ervan uit dat de temperatuur van het slachtoffer 37°C was toen de dood intrad. Wanneer is de moord gebeurd?

Alvast bedankt.

Groetjes Rob

Rob
3de graad ASO - zaterdag 12 maart 2005

Antwoord

Beste Rob,

De formule is dus:



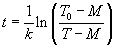
Vul deze formule nu in voor de 2 tijdstippen waarvan je de gegevens hebt.
De eerst keer zit je op een tijdstip 't' na de moord.
De tweede keer zit je op een tijdstip 't+1' na de moord, vermits t in uren wordt uitgedrukt.

Je hebt dan:



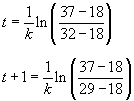
Nu heb je dus 2 vergelijkingen in 2 onbekenden (t en k). Dit is een oplosbaar stelsel.

Kan je nu verder?

mvg,
Tom

zaterdag 12 maart 2005

©2001-2024 WisFaq