Tweedegraadsformule

een parabool wordt gedefinieerd als de verzameling punten die even ver van een gegeven punt (het brandpunt ) en een gegeven lijn ( de richtlijn ) afliggen. Neem als brandpunt F (0,3) en als richtlijn R : y = -3 en laat zien dat bovenstaande definitie een tweedegraadsformule oplevert.

irem
Leerling bovenbouw havo-vwo - zaterdag 12 maart 2005

Antwoord

Bekijk onderstaande tekening:



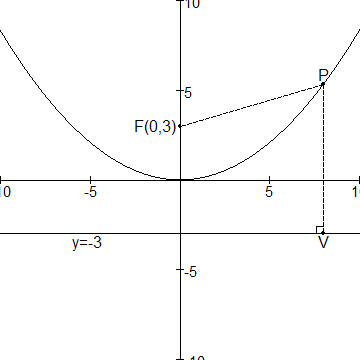
F is het brandpunt (0,3).
Ook is de lijn y=-3 getekend.
P(x,y) is een punt op de parabool.
De afstand van P tot de lijn y=-3 is gelijk aan y--3=y+3.
De afstand van P tot F is Ö(x²+(y-3)²)
Deze twee afstanden moeten gelijk zijn, dus:
y+3=Ö(x²+(y-3)²)
(y+3)²=x²+(y-3)²
y²+6y+9=x²+y²-6y+9
6y=x²-6y
12y=x²
y=¹/₁₂x², en dat is een "tweedegraadsformule".

zaterdag 12 maart 2005

©2001-2024 WisFaq