Bewijs met omtrekshoek en middelpuntshoek

Er is een cirkel. Op de cirkel liggen punt A en C.
Punt B ligt buiten de cirkel. Van hoek BAC raakt AB de cirkel. Hoek MAB is 90 graden. Te bewijzen dat hoek BAC gelijk is aan de 1/2 * boog AC.
Ik weet dat de lengte van de boog gelijk is aan de middelpuntshoek, stel nu dat boog AC 110 is, dan is hoek AMC ook 110 graden; maar dan kan hoek BAC toch nooit 55 graden zijn; hoek BAC is stomp als ik de situatie teken.

Li-an
Leerling onderbouw vmbo-havo-vwo - zondag 20 februari 2005

Antwoord

Eerst mijn tekening:

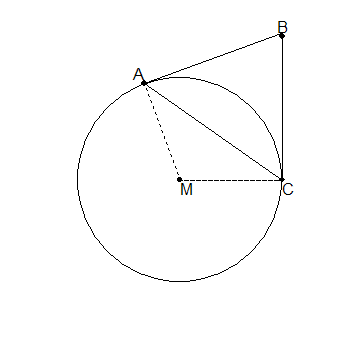
Dan:
ÐAMC=110°
Driehoek AMC is gelijkbenig, dus ÐMAC=ÐMCA=...(vul in)
ÐMAB=90°
Dus ÐBAC=90°-ÐMAC=...

zondag 20 februari 2005

©2001-2024 WisFaq