Rationale oplossing van een vergelijking

Heeft de vergelijking a^b = b^a andere rationale oplossingen voor a en b dan de triviale (a=b) en a=2,b=4 en a=4,b=2 ?
Duidelijk, dat er geen andere gehele oplossingen zijn.
Ik kwam niet verder dan dan dit equivalent is met de vraag of ln(x)/x = a twee rationale oplossingen heeft voor een a tussen 1 en 1/e. NB a moet hierbij in elk geval irrationaal zijn (want e^n is irrationaal voor n rationaal).

Arno
Docent - zondag 16 januari 2005

Antwoord

Als de vraag inderdaad is: heeft ln(x)/x=a oplossingen voor 1/ea1 dan is het antwoord nee. Immers:
Kies f(x)=ln(x)/x, dan
f'(x)=(1/x*x-1*ln(x))/x²=(1-ln(x))/x
f'(x)=0 levert ln(x)=1, dus x=e.
f(e)=1/e.

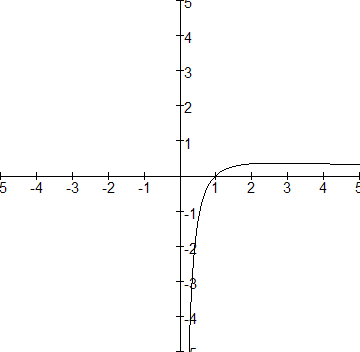
Uit bovenstaand plaatje (en/of het tekenschema van f) valt dan gemakkelijk in te zien dat 1/e het absolute maximum is van ln(x)/x.

zondag 16 januari 2005

Re: Rationale oplossing van een vergelijking

©2001-2024 WisFaq