Viervlak

een snijdt een viervlak met een vlak dat evenwijdig is met 2 overstaande ribben. bewijs dat de snijpunten van dit vlak met de andere ribben de hoekpunten zijn van een parallellogram.( ik weet nie hoe ge die tekening hierop moet zetten) Ik heb dit al:
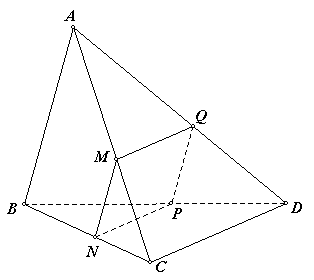
gegeven:* vlak MNPQ = aen ais //AB en ook // metCD
gevraagd:Is MNPQ parallellogram?
oplossing: AB // vlak a
AB // vlak ABC
Dus AB // (aÇ vlak ABC) en AB // MN

giovan
3de graad ASO - zaterdag 15 januari 2005

Antwoord

Je schrijft in je oplossing dat
(1) AB // a (=MNPQ)
(2) AB // ABC (inderdaad, een lijn in een vlak is ermee evenwijdig)

Je gebruikt dan (stilzwijgend) de stelling (*):

Als een lijn evenwijdig is met twee snijdende vlakken, dan is die lijn evenwijdig met de snijlijn van die vlakken.

Heb je je dat gerealiseerd, EN ook, heb je die stelling gehad?

De conclusie uit (1) en (2) is dan (inderdaad):
AB // MN
Kan je nu ook bewijzen, dat AB // PQ? Min of meer op dezelfde manier ...?
Waarom is dan MN // PQ?
Waarom is ook PN // QM?
Waarom mag je dan concluderen, dat MNPQ een parallellogram is?

(*) Ik zou me kunnen voorstellen dat de stelling niet behandeld is.
In plaats daarvan bekijken we de volgende figuur.

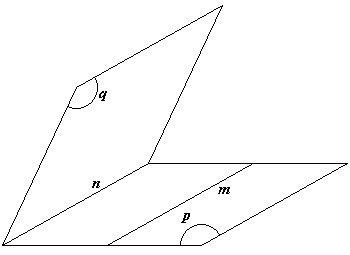
Daarin zijn we uitgegaan van een vlak p met daarin een lijn m.
We snijden het vlak p met een vlak q, waarvan we weten dat het evenwijdig is met de lijn m.
We krijgen zo een snijlijn n.
Er zijn nu drie mogelijkheden voor m en n:
(i) m kruist n
(ii) m snijdt n
(iii) m // n
Beredeneer (bewijs) dat (i) en (ii) NIET mogelijk zijn.
Blijft dus over (iii): m // n.
Wel, gebruik deze stelling om te bewijzen dat AB // MN.
Geef daarbij aan welke vlakken overeenkomen met p en q, en welke lijnen met m en n.

Ben je er zo uit?

zaterdag 15 januari 2005

Re: Viervlak

©2001-2024 WisFaq