Limiet

wat is de limiet van (x®0 van de functie ln(1+xcos(x))-x + 0,5 x^2 + 1/6 x^3)/(e^(x^4)-1)??

bart v
Student universiteit - woensdag 12 januari 2005

Antwoord

Beste Bart,

Ik neem aan dat het volledige eerste gedeelte in de teller staat, want je hebt geen openingshaak voor de teller geschreven.

In dat geval krijg je, als je gewoon 0 invult, de onbepaaldheid 0/0.
Daar zijn 2 methodes voor:
- De regel van L'Hoptital: teller en noemer afleiden, maar dan zal je wel een heel tijdje 0/0 blijven houden.
- Een Taylor-reeksontwikkeling.

Als ik zie hoe je oefening eruit ziet ben ik er bijna zeker van dat het de bedoeling is dat je met Taylor ontwikkelt.

De reeksontwikkeling van ln(1+xcos(x)) tot op orde 4 rond 0 is:
x + x²/2 - x³/6 + x⁴/4
De reeksontwikkeling van e^(x^4) tot op orde 4 rond 0 is:
x⁴ + 1

Als we deze reeksontwikkelingen dan invullen zal je zien dat er erg veel wegvalt:



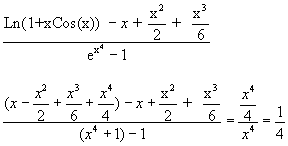
De limiet is dus 1/4.

mvg,
Tom

woensdag 12 januari 2005

Re: Limiet

©2001-2024 WisFaq