Re: Sigmoïde curve

Dit is een reactie op vraag 32428

Bedankt voor uw antwoord. Logistische groei lijkt aanmemelijk.

Maar ... de leraar wiskunde zei met nadruk dat hier sprake is van exponentiële groei vóór een bepaald omslagpunt en ná dat omslagpunt (de groei stagneert dan bij de asymptoot van 2050). Dus eerst toenemende expon. groei, daarna expon. afnemende groei.

Bedankt voor uw tijd. De formule die logistische groei beschrijft zou goed moeten zijn.

Jeroen

Jeroen
Student hbo - woensdag 12 januari 2005

Antwoord

Eerst maar even een plaatje van de data, en ook maar gelijk een grafiekje van die logistische groei.
Wat veel gebeurt is dat men logistische groei probeert te benaderen met twee exponentiele grafieken:
linkerstuk y=c·g₁^t of zoiets en rechterstuk y=max-c·g₂^t

Ik kies nu voor een iets andere vorm om de twee grafieken bij t=40 netjes te laten aansluiten:
links:
y=1200·g₁^t-40
rechts
y=2050-(2050-1200)·g₂^t-40=2050-850·g₂^t-40.

Het enige wat we nu nog moeten doen is enigszins geschikte waarden voor g₁ en g₂ vinden.

Eerst het linkerstuk. Je kunt in het plaatje zien dat de boel op het eerste gedeelte (t=15 tot t=30) niet zo aardig exponentieel verloopt. Ik ga dus proberen de exponentiele functie pas door t=20 te laten lopen en niet door t=15
Goed, we vullen t=20 en y=200 in en krijgen:
200=1200·g₁^20-40, dus g₁^-20=1/6, dus g₁=6^1/20=1,094.

Nu het tweede stuk.
Ik vul t=70 en y=2000 in:
2000=2050-850·g₂^70-40
Dus 850·g₂³⁰=50
Dus g₂³⁰=50/850, waaruit volgt
g₂=(50/850)^1/30=0,91

Hieronder in een plaaatje staan in rood de logistische benadering en in groen de "exponentiele"


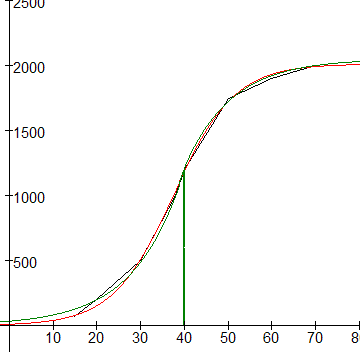
Best wel aardig voor wat handmatig gepruts zonder het geweld van CurveExpert, vind ik.

donderdag 13 januari 2005

©2001-2024 WisFaq