Gelijkvormigheid

Gegeven: driehoek ABC is rechthoekig in C en de hoek A is 18°. Vanuit C past men op AC de lengte BC af. Noem dit punt D. Uit D tekent men loodrecht op AB en snijpunt E de driehoek ADE is gelijkvormig met ABC want rechthoekig in E en A is gemeenschappelijk.


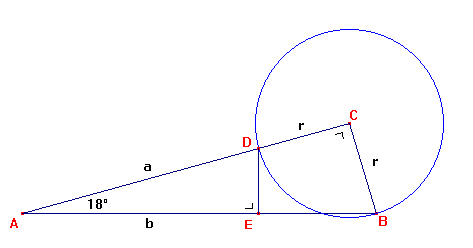
Vraag: wat is de gelijkvormigheidsfactor?

Olivie
Ouder - woensdag 5 januari 2005

Antwoord

Je kan er geraken mbv goniometrische eigenschappen in rechthoekige driehoeken.

Cosa=(aanliggende rechthoekszijde)/(schuine zijde)
Sina=(overstaande rechthoekszijde)/(schuine zijde)

Beschouw de grote driehoek:
a = AC (en niet AD, kan verwarrend zijn in de tekening)
b = AB (dus niet AE)
r = DC = BC
AD = AC-AD = a-r

Cos(18°)=a/b = a=b*cos(18°)
Sin(18°)=r/b = r=b*sin(18°)

De evenredigheidsfactor is volledig bepaald als je de verhouding kent tussen 2 overeenkomstige zijden - wij nemen de schuine zijde.

In de kleine driehoek is dat a-r
In de grote driehoek is dat b
Evenredigheidsfactor:
(a-r)/b = (b*cos(18°)-b*sin(18°))/b
= b(cos(18°)-sin(18°))/b
= cos(18°)- sin(18°)

Dit is bij benadering 0.65

mvg,
Tom

woensdag 5 januari 2005

©2001-2024 WisFaq