Afstand tussen punten op archimedische spiraal

Stel; ik moet een x aantal gaten maken in een schijf (vb: diameter=100mm). De gaten hebben een diameter van 6 mm. Ik wil dat door de schijf in 1 richting te roteren dat alle gaten voor een statisch gepositioneerd 'oog' komen. Dit is niet moeilijk als die gaten zich op een cirkelomtrek bevinden met een straal gelijk aan de afstand van het oog tot het midden van de schijf. MAAR, ik moet zoveel gaten maken in deze schijf, dat deze niet allemaal op 1 cirkel kunnen op deze schijf. Om dit op te lossen, wil ik gaten maken in de schijf in de vorm van een spiraal en door de schijf EN te roteren EN te transleren kan ik alle gaten voor dat 'oog' krijgen. Mijn vraag: als ik een constante draaisnelheid en translatiesnelheid aan die schijf geef,met welke formule kan ik dan de steeds afnemende straal berekenen van de spiraal om zo de steeds afnemende afstand tussen de gaten bij rotatie (van buitencirkel naar binnencirkel) te berekenen?

Ik hoop dat m'n vraag duidelijk genoeg is

Met vriendelijke groet,

Erik

Erik
Student hbo - vrijdag 10 december 2004

Antwoord

Dag Erik,

Als de translatiesnelheid constant is, en de translatiebeweging is 'radiaal' gericht, dan is de afnemende straal gewoon lineair afnemend.
Voorbeeld: kies het centrum van de schijf als oorsprong, noem de hoeksnelheid van de rotatie h (rad/sec), en de translatiesnelheid v (m/s).
Op tijdstip t=0 zit het oog voor gat 1, op afstand r1 van het centrum.
Op tijdstip t zit het oog voor gat 2.
De afstand van gat 2 tot het centrum is dus r1-v·t
Na t seconden is gat 1 over een hoek h·t gedraaid.
De afstand d van de gaten 1 en 2 bereken je dan met de cosinusregel:
d² = r1² + (r1-v·t)² - 2·r1·(r1-v·t)·cos(h·t)


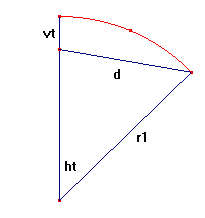
Maar eerlijk gezegd begrijp ik niet hoe je met een spiraalvorm meer gaten kunt maken: hoe dichter bij het centrum, hoe meer de gaten elkaar in de weg zitten.
Maar hopelijk heb je toch iets aan deze uitleg.
groet,

vrijdag 10 december 2004

©2001-2024 WisFaq