De oogbalsituatie

Hallo,

Ik moet voor een Practische Opdracht de oogbalsituatie bewijzen. (Voor de vragen kijk op: Oogbal)

Ik heb er al erg veel tijd aan besteed maar ik zie het maar niet. Ik heb Cabri Geometre gebruikt om de situatie te simuleren, maar zonder resultaat.

Kan iemand me misschien helpen om dichter bij de oplossing te komen? Alle hulp is welkom...

Alvast enorm bedankt

Mark
Leerling bovenbouw havo-vwo - zaterdag 2 oktober 2004

Antwoord

Op de formulekaart staat:

Een raaklijn aan een cirkel staat loodrecht op de verbindingslijn van middelpunt en raakpunt.

M.b.v. deze eigenschap is het mogelijk de raaklijnen in de tekening te construeren.
B.v. de raaklijnen vanuit B aan de cirkel met middelpunt A kun je als volgt construeren.
Als T een van de gezochte raakpunten is dan moet volgens de stelling van Thales T liggen op een cirkel met middellijn AB. Maar T ligt ook op de cirkel met middelpunt A dus T is een snijpunt van de cirkel met middelpunt A en de cirkel met middellijn AB.

In onderstaand plaatje zie je het resultaat.



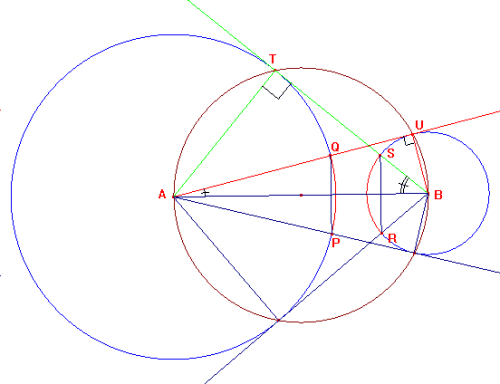
Voor de rest van de opdracht kun je het best eerst proberen te bewijzen dat lijnstuk PQ even lang is als lijnstuk SR.
Omdat de hele figuur alleen afhankelijk is van de stralen van beide cirkels en de lengte van lijnstuk AB kun je hier namen aan geven.
Noem de straal van de cirkel met middelpunt A: R
Noem de straal van de cirkel met middelpunt B: r
Noem de lengte van het lijnstuk AB: d.

Bekijk nu eerst eens driehoek ATB. Deze is rechthoekig in T, AT=R en AB=d.
Verder geldt: SR staat loodrecht op AB, en AB deelt SR middendoor. S ligt op TB zo, dat SB=r.
Lukt het je nu met gelijkvormigheid of goniometrie de lengte van lijnstuk SR uit te drukken in R, r en d?
Bekijk dan driehoek AUB en probeer dan ook de lengte van lijnstuk PQ uit te drukken in R, r en d.
Levert dit hetzelfde op?

Probeer daarna, gewapend met het feit dat PQ en SR evenlang zijn te laten zien dat in het algemeen de lengtes van de bogen PQ en SR niet gelijk zijn.

zaterdag 2 oktober 2004

©2001-2024 WisFaq