De diagonalen in het vierkant in de parallellogram?

Hoe kan ik bewijzen dat het snijpant van de diagonalen in het vierkant in het parallellogram hetzelfde snijpunt is als de diagonalen van het parallellogram zelf?

B. de
Leerling bovenbouw havo-vwo - vrijdag 24 september 2004

Antwoord

Goeiedag

Ik neem aan dat je bedoelt dat elk hoekpunt van het vierkant, op een andere zijde van het parallellogram moet liggen. Dat was niet geheel duidelijk. Je kan het probleem zowel algebraïsch oplossen, als meetkundig.

A) ALGEBRAISCH

Je tekent best eerst een vierkant en daarna het parallellogram erond:



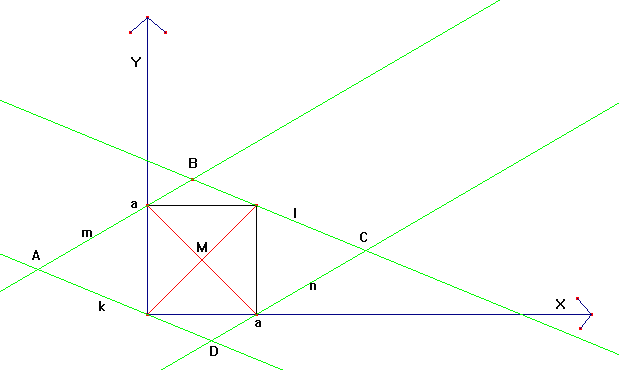
Op de tekening heb ik reeds de x-as en de y-as getekend. Het punt M(a/2,a/2) is het middelpunt van het vierkant. Je moet bewijzen dat dit punt ook het middelpunt is van de par.

Dit kan door te bewijzen dat M op beide diagonalen van de par ligt. Je kan dit door te bewijzen dat A,M,C en B,M,D

collineair zijn (3 punten zijn collineair als ze op éénzelfde rechte liggen). Stel eerst de vgl op van de rechten k,l,m & n:

k: y=px
l: y=p(x-a)+a
m: y=qx+a
n: y=q(x-a)

Zoek vervolgens de coördinaat van A, B, C & D. Daarna bewijs je dat A,M,C & B,M,D collineair zijn.

B) MEETKUNDIG

zie tekening:



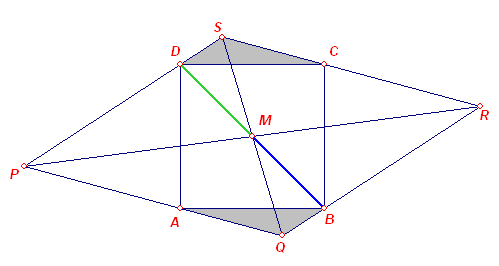
Neem aan dat M het snijpunt is van de diagonalen van het parallellogram. Je moet bewijzen dat M ook het middelpunt van het vierkant is. De driehoeken AQB en CSD zijn congruent (HZH), met Z = zijde van het vierkant. Daaruit volgt dat |QB| = |SD|. Je moet proberen te bewijzen dat de hoek DMB gelijk is aan 180 graden, want daaruit volgt dat het middelpunt van het par ook het middelpunt van het vierkant is. Dit kan door te bewijzen dat hoek M in driehoek MQB en hoek M in driehoek DMB gelijk zijn. Probeer dit zelf eens (tip: bewijs dat DMQB en DMSD congruent zijn).

Groetjes

Igor
zaterdag 25 september 2004

Re: De diagonalen in het vierkant in de parallellogram?

©2001-2024 WisFaq