Extreme waarden van een functie berekenen

Hey!
ik heb de volgende functie:
f(x)=((x²)-9x+13)/(x-5)
deze functie is ook te schrijven als:
f(x)=x-4-(7/(x-5))

Nu is mijn vraag: hoe bereken ik algebraïsch de (locale) extreme waarden van f en voor welke waarden van x worden ze aangenomen. En als ze niet bestaan dient duidelijk gemaakt te worden waarom ze niet bestaan.
Ik snap er helemaal niks van, ik hoop dat jullie me kunnen helpen.

Bij voorbaat dank!!

Pieter
Leerling bovenbouw havo-vwo - zondag 8 augustus 2004

Antwoord

Hallo Pieter,

Uit het feit dat de functie te schrijven is als



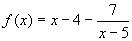
volgt dat deze functie twee asymptoten heeft

(1) een vertikale asymptoot x = 4

(2) een scheve asymptoot y = x-4

Als we algebraïsch de extreme waarden van een functie moeten bepalen dan moeten we f’(x)=0 oplossen en het tekenverloop van f’(x) onderzoeken.

Bij deze functie kun je aantonen dat f'(x) voor elke waarden van x¹5 positief is. Er is dus geen lokaal minimum of maximum.

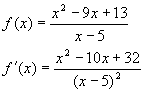
Een breuk = 0 als de teller = 0

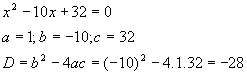
De teller is een dalparabool zonder nulpunten. Er geldt dus dat de teller voor elke x groter is dan 0.
De noemer van de breuk is voor x¹5 ook positief. Dus f'(x)>0 voor x¹5

wl
zondag 8 augustus 2004

©2001-2024 WisFaq