Oplossing van een vergelijking met de natuurlijke logaritme

Ik kom niet uit deze vraag;

Wat is de oplossing van de vergelijking;

ln (x+3)/x = 3 ln 2x - ln x³ - ln x

Het antwoord is x=5, maar kom er niet op

Bedankt alvast,
Groetjes

mirell
Leerling bovenbouw havo-vwo - donderdag 1 juli 2004

Antwoord

Het antwoord is niet x=5, vul dat maar eens in het linker- en het rechterlid in, je komt niet hetzelfde uit.
Het antwoord is bij benadering x = 5,392001152.

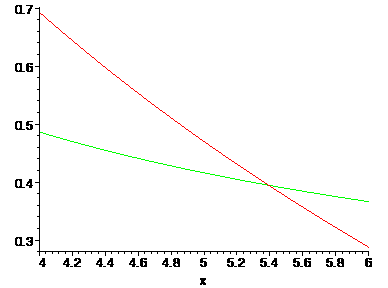
De rode grafiek is die van ^ln(x+3)/_x en de groene die van 3·ln(2x) - ln(x³) - ln(x).
Exact kun je het snijpunt niet bepalen, want er is geen formule die ln(x+3) 'vergemakkelijkt', wel geldt dat ln(a) + ln(b) = ln(ab) en dat ln((c)^d) = d·ln(c), wat ln(2x) en ln(x³) laat herschrijven tot ln(2) + ln(x) en 3·ln(x) maar daar heb je niet zoveel aan aangezien het linkerlid zich niet laat vereenvoudigen.

Indien je (zoals Anneke opmerkte) de vergelijking ln((x+3)/x) = 3·ln(2x) - ln(x³) - ln(x) bedoelde, dan gaat 't wel... let dus op de haakjes!
Namelijk ln(x+3) - ln(x) = 3·ln(2x) - ln(x³) - ln(x)
<=> ln(x+3) = 3·(ln(2) + ln(x)) - 3·ln(x)
<=> ln(x+3) = 3·ln(2)
<=> x + 3 = e^3·ln(2)
<=> x + 3 = e^ln(8)
<=> x + 3 = 8
<=> x = 5

donderdag 1 juli 2004

©2001-2024 WisFaq