Geheeltallig lineair programmeren

Hoi, ik moet een wiskunde opdracht maken maar ik begrijp 1 opgave niet! Ik heb van alles geprobeerd maar ik kom er helemaal niet uit. De opgave luid:

De kleine rederij Via Marre is gevestigd in het havenplaatsje Porto Marino. In verband met jeugdkamp krijgt Via Marre de opdracht om binnen 1 dag 258 personen en 12000 kg vracht over te brengen naar het voor de kust gelegen eilandje Solatio.

Via Marre beschikt over twee scheepjes: de Aringa die ruimte heeft voor 16 passagiers en 400 kg vracht, en de Balena die ruimte heeft voor 6 passagiers en 2000 kg vracht. De argina kan in een dag ten hoogste 20 keer heen en weer varen naar Solatio, de Balenta ten hoogste 15 keer. een keer heen en weer varen met Argina kost de rederij 1.000.000 lire, en met de Balena 400.000 lire.

Via Marre streeft er naar elke opdracht uit te voeren met zo laag mogelijke kosten.

1. Stel dat de Argina x keer heen en weer laat varen en de Balena y keer. Welke voorwaarden gelden voor x afzonderlijk en welke voorwaarden gelden voor y afzonderlijk?
   
   
2. De informatie over de passagierscapaciteit en de vracht-capaciteit van de twee scheepjes leidt tot twee beperkende voorwaarden. Toon aan dat deze twee beperkende voorwaarden kunnen worden beschreven door 8x+3y129 en x+5y30.
   
   
3. Toon aan dat, als de opdracht met zo laag mogelijke kosten wordt uitgevoerd, telkens de passagierscapasiteit en de vrachtcapaciteit volledig benut worden.
   
   
4. De plannen zijn net gemaakt als er bericht komt dat er niet 258 maar slechts 240 personen vervoerd moeten worden. De hoeveelheid vracht blijft 12.000 kg. Men vraagt zich af hoe de opdracht nu met zo laag mogelijke kosten kan worden uitgevoerd. geef antwoord op deze vraag. Vermeld in je antwoord de kosten en geef aan of de passagierscapaciteit en de vrachtcapaciteit volledig benut worden. geef ook je gemaakte berekening.

Ik hoop dat ik hiermee geholpen kan worden, het is een erg lange som en best ingewikkeld. Ik hoop snel wat te horen

Alvast bedankt,
Groetjes

patric
Leerling bovenbouw havo-vwo - dinsdag 15 juni 2004

Antwoord

Hallo Patricia,

(1)
De Argina kan hoogstens 20 keer op en neer varen dus x20
De Balena kan hoogstens 15 keer op en neer varen dus y15

(2)
Voor de passagierscapaciteit geldt 16x+6y258 Û 8x+3y129
Voor de vrachtcapaciteit geldt 400x+2000y12000 Û x+5y30

(3)
De doelfunctie is K=x+0,4y (K in miljoen lire)
We hebben te maken met de volgende beperkingen:



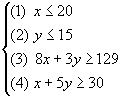
De hoekpunten van het toegestane gebied zijn (10,5;15),(15;3),(20;2) en (20;15).
In het punt (15;3) zijn de kosten minimaal. K_min=15+0,4.3=16,2 miljoen lire.
Omdat dit punt het snijpunt is van de beperkende voorwaarden (3) en (4) geldt ook dat de passagierscapaciteit en de vrachtcapaciteit volledig benut worden.

(4)
De beperkende voorwaarden worden nu:



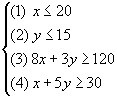
De hoekpunten van het toegestane gebied zijn (9,4;15),(13,8;3,2),(20;2) en (20;15).
In het punt (13,8;3,2) zijn de kosten minimaal. Maar omdat x en y aantallen zijn moet je gaan zoeken naar een roosterpunt in het toegestane gebied dat hier zo dicht mogelijk bij ligt.

Omdat dit punt niet het snijpunt is van (3) en (4) wordt de passagierscapaciteit en de vrachtcapiciteit niet volledig benut. De rest laat ik aan jouw over.

wl
woensdag 16 juni 2004

©2001-2024 WisFaq