Goniometrische vergelijkingen oplossen

Hallo,

Ik ben al een tijdje bezig met deze vergelijkingen, maar ik krijg het niet helemaal voor elkaar kunnen jullie helpen?

De vergelijkingen:

1. -2sin($\pi$-X)=0
2. 3cos(x+$\pi$) = -1

bij de eerste kom ik een eind, maar ik krijg niet alles eruit, de tweede lukt niet echt.

1. -2sin($\pi$-x)=0
sin($\pi$-x) =0/-2 = 0
$\pi$-x =sin_IN√(0) = 0
dan krijg ik dit eruit

$\pi$ - x = 0+k·2$\pi$
-x = -$\pi$+k·2$\pi$

nu ben ik nog op zoek naar de andere keuze die moet leiden tot:

$\pi$ - x = $\pi$ +k ·2$\pi$
-x = 0 +k ·2$\pi$

hoe kan ik aan die tweede lijst komen, ik zie niet waar die $\pi$vandaan komt.

alvast bedankt voor uw hulp.

groetjes

peter
Leerling mbo - maandag 7 juni 2004

Antwoord

Ik vermoed dat je probleem te maken heeft met het volgende (even voor het gemak in graden!):

sin $\alpha$ = 0,5, wat is $\alpha$?

Met je rekenmachine (of uit je hoofd!) zou je kunnen constateren dat moet gelden:

$\alpha$ = 30°

..of als je wilt:

$\alpha$ = 30° + k·360° (met k$\in$$\mathbf{Z}$)

Het is immers een periodieke functie, dus als je alle mogelijke oplossingen wilt geven, dan zal het zoiets moeten worden.

Maar toch klopt het niet... want er geldt ook:

sin 150° = 0,5

Dus heb ik nog een oplossing! Aan dit plaatje kan je zien hoe dat zit:



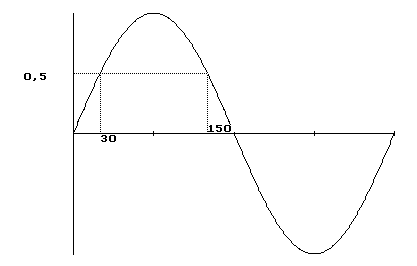
Dat is dus 180°-30°=150°. Dat geldt dus (bijna) altijd. In meer algemene (en nu dan met radialen) geldt:

sin $\alpha$ = p
$\alpha$ = t + k·2$\pi$ of $\alpha$ = $\pi$-t + k·2$\pi$
met k$\in$$\mathbf{Z}$ en sin(t)=p

Voorbeeld
sin x = 0,5
x=¹/₆$\pi$ + k·2$\pi$ of x=⁵/₆$\pi$ + k·2$\pi$, met k$\in$$\mathbf{Z}$

Voorbeeld
sin($\pi$-x)=0
$\pi$-x=0 + k·2$\pi$ of $\pi$-($\pi$-x)=0 + k·2$\pi$
x=$\pi$ + k·2$\pi$ of x=0 + k·2$\pi$
x=0 + k·$\pi$

O ja... bij cosinus gebeurt in feite hetzelfde maar dan anders:



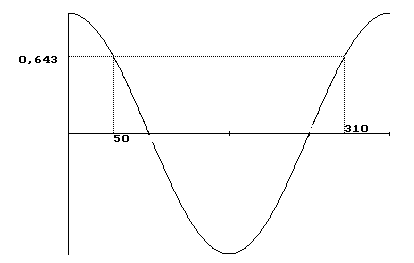
Nu geldt:
cos $\alpha$ = p
$\alpha$ = t + k·2$\pi$ of $\alpha$ = 2$\pi$-t + k·2$\pi$

Hopelijk helpt dat...

maandag 7 juni 2004

©2001-2024 WisFaq