Integraalfunctie

Ik heb bijzondere moeite met het oplossen van deze oefening.Elke poging resulteert in een absurd resultaat:

Kijk na dat y=òf(t)sinw(x-t)dt met als interval 0 tot x een specifieke oplossing is van de diff.vergelijking y''-w²y=f(x).

Alvast bedankt,

Kevin

kevin
Student universiteit - donderdag 22 april 2004

Antwoord

Algemeen heb je volgende eigenschap voor G(x) een integraal waarbij de variabele x zowel in de bovengrens als het integrandum voorkomt.
G1(x) is de eerste afgeleide van G(x) naar x dus G1(x)=D(G(x)).
G2(x) is de tweede afgeleide van G(x) naar x.


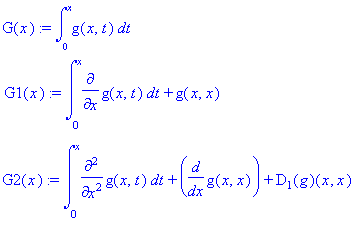
Hierin staat D₁(g)(x,x) voor de afgeleide naar het eerste argument.

Dus toegepast op je voorbeeld krijg je:


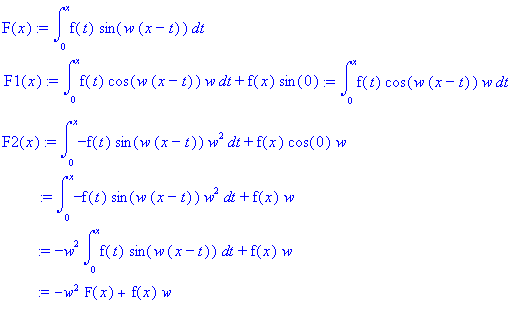
Zodat y''+w²y=f(x)w

Dit doet vermoeden dat je opgave fout was.
Als we vertrekken van de differentiaalvergelijking die jij hebt opgegeven dan bekijk je eerst de homogene vergelijking.
y''-w²y=0
en bepaal hiervan de karakteristieke vergelijking:
s²-w²=0
deze vergelijking heeft twee oplossingen nl. s=w of s=-w.
Bijgevolg is de algemene oplossing y_g=c1*exp(-w*x)+c2*exp(w*x)
De particuliere oplossing bepaal je dan vertrekkend van de vorm van het rechterlid nl. y_p=c*f
met c, c1 en c2 nog nader te bepalen constanten.

Mvg,

Els
maandag 26 april 2004

©2001-2024 WisFaq