Kruisgewelven

Hoe kan de oppervlakte van een kruisgewelf worden berekend?

tvh
Iets anders - woensdag 27 maart 2002

Antwoord

Ik neem aan dat je met 'Kruisgewelf ' een gewelf bedoelt dat ontstaat als twee ton-gewelven elkaar loodrecht 'kruisen'. Ton-gewelven hebben de vorm van halve cilinders. Meer over gewelven op bogen en gewelven.

Voor de berekening neem ik eerst twee halve cilinders met straal 1 en we kijken alleen naar het stuk waar de cilinders echt door elkaar gaan. Dat ziet er in perspectief van boven dan uit als in de figuur hieronder; al kijk je gewoonlijk niet zo op gewelven neer, maar zie je ze alleen van onderen.



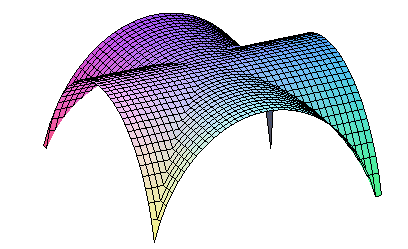
We bekijken nu het gewelf in bovenaanzicht, dat is het vierkant in de volgende figuur.



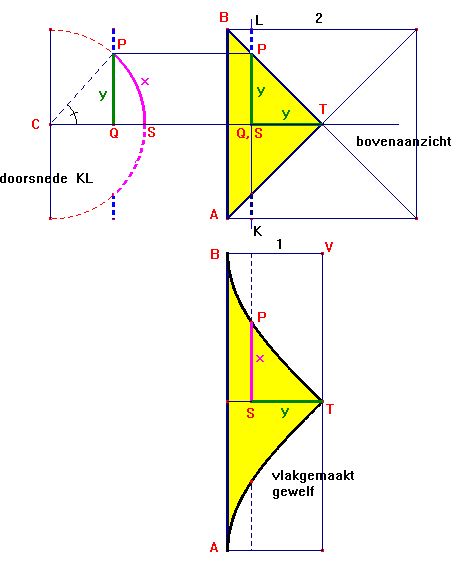
Driehoekig stuk ABT in het vierkant is in werkelijkheid gebogen; vlakgerold staat het er onder. De halve cirkel links is de doorsnede van de halve cilinder die van links naar rechts loopt. P is een (variabel) punt op de snijlijn van de twee cilinders.

Van ABT in het onderste deel van de figuur moeten we de oppervlakte bepalen.

Boog SP in de doorsnede heeft de werkelijke lengte x van wat in het bovenaanzicht lengte y = QS heeft.
Er geldt ook nog ST = QP = y.
Omdat de straal van de halve cirkel 1 is, zie je uit de doorsnedefiguur direct dat y = sin(x).
De gebogen lijn TPB in het uitgerolde gewelf is dus de grafiek van de sinusfunctie, met lijn TV als X-as.
TV = /2 en de oppervlakte van TPBV kun je uitrekenen door integreren van sin(x) over het interval [0 , /2] ; dat geeft 1.
Dan is dus opp. ABT (in het uitgerolde gewelf) gelijk aan -2.
Als je R als straal neemt voor de cilinders, in plaats van 1, moet dit met R² worden vermenigvuldigd; omdat er vier van die stukken in het gewelf, zijn vind je als totaal:

Oppervlakte kruisgewelf bij straal R : 4R²( -2).

---

Slotopmerking:
Als de dwarsdoorsnede van het gewelf niet cirkelvormig is, dan gaat het eigenlijk precies zo, behalve dat je dan niet meer met y = sin(x) kunt werken.
Maar juist daardoor wordt het snel ingewikkeld!
Als de doorsnede een parabool is, is het verband tussen y en x nog net te berekenen met een vrij ingewikkelde formule. Zelfs kan de integraal daarvan nog uitgerekend worden.
Maar als de doorsnede een ellips is, bestaat er niet eens een formule die y in x uitdrukt!

aad
dinsdag 2 april 2002

©2001-2024 WisFaq