Oppervlakte van een dodecaeder
Hallo,
Ik ben bezig de formule waarmmee je de oppervlakte van een dodecaeder kunt berekenen te herleiden. De formule waar ik op uit moet komen is 3r2Ö(25+10Ö5)
Mijn berekening:
sin a=h/s cos a=1/2r/s
h=s· sin a s=1/2r/cos a
Oppv. ABC=1/2(h·1/2r)
=1/2(sin 54º·s·1/2r)
=1/2(sin54º·(1/2r/cos 54º)·1/2r)
Dit is de formule voor de driehoek ABC. Maar in een vijfhoek heb je tien van zulke driehoeken, dus doe je de formule keer tien. En in een dodecaëder zitten twaalf regelmatige vijfhoeken.Dus om het aantal van deze ABC driehoeken in een dodecaëder te weten te komen doe je:
12·10=120 ABC driehoeken.
Als je dus de oppervlakte van de hele dodecaëder wilt weten, moet je de formule, waarmee je de oppervlakte berekent van de ABC driehoek , keer het aantal ABC driehoeken in een hele dodecaëder doen. En dat was honderdtwintig!
Dus de formule voor de oppervlakte van de hele dodecaëder is:
120·(1/2(sin 54º·(1/2r/cos 54º)·1/2r)
=60(sin54(1/2r/cos54)·1/2r)
Deze formule komt wel in de buurt maar ik zou echt niet weten hoe ik toch tot de formule 
Weten jullie hoe het mij wel zal lukken???
Ik weet ook niet hoe ik kan bewijzen dat een regelmatige vijfhoek ook werkelijk uit 5 gelijkbenige driehoeken bestaat met hoeken 72°
Zouden jullie me op weg kunnen helpen???!!!
Wanhopige...
marlee
Leerling bovenbouw havo-vwo - donderdag 26 februari 2004
Antwoord
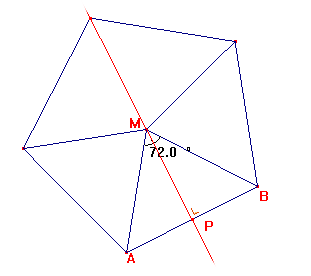 Volgens mij staat een groot deel van je antwoord op Oppervlakte regelmatige vijfhoek.
De hoeken van de 5 driehoeken van de vijfhoek laten zich eenvoudig berekenen. Als je naar het 'middelpunt' kijkt. 5 hoeken samen 360°, dus 72° per hoek. De driehoeken zijn gelijkbenig.. enz.
Hopelijk helpt dat.
zaterdag 28 februari 2004
©2001-2024 WisFaq
|