Rendement berekenen van beleggingen

Ik ben bezig voor mijn stage bij een vermogensbeheerbedrijf. Ik heb gegevens en rendementen van obligaties, staatsleningen, aandelen enz. Maar hoe wordt zo´n rendement berekend? Ik heb al allerlei boeken nagezocht, maar kan het goede niet vinden. Heb je een formule ervoor? als dat zo is, heb je dan een voorbeeld en uitleg erbij?
Alvast bedankt,
Sanne

Sanne
Student hbo - donderdag 12 februari 2004

Antwoord

Beste Sanne,

In algemene termen is het rendement de winst (opbrengst, intrest) die je uit een belegging haalt op jaarbasis in verhouding tot het ingelegd kapitaal (het geld dat je gebruikt hebt om te beleggen). Het probleem is echter dat er geen eenduidige formule is voor elke beleggingsvorm. Zelfs voor sommige beleggingsvormen heb je meerdere formules.

Beleggingen zonder waardeverandering

Dit zijn alle beleggingen die niet afhankelijk zijn van waarde- of koersveranderingen. Dus alles behalve obligaties, aandelen en afgeleide producten. Wat overblijft zijn eigenlijk allemaal beleggingen zonder risico. Bij deze beleggingen spreekt men bijna nooit over het rendement, omdat het rendement bijna steeds gelijk is aan de intrestvoet en in de gevallen waar dit niet zo is, is er slechts een minimale afwijking met de intrestvoet.

Het rendement kan je dan berekenen als het bedrag dat je als intrest krijgt gedeeld door het ingelegd bedrag. Stel: staatslening van € 10.000 over 2 jaar aan 5%.
Intrest van de eerste coupon na 1 jaar is: € 500
Rendement = 500 / 10.000 = 5% (of intrestvoet).
Voor het tweede jaar is dit gelijk.
 
Laten we eens kijken wat er gebeurd als de intrest gekapitaliseerd wordt (dus geen coupons, intrest wordt uitgekeerd op de vervaldag van de belegging). Nemen we terug dezelfde gegevens.Het tweede jaar is de intrest dan 5% over 10.000 + 500 = 525
Rendement is nu niet op 10.000, maar op 10.500 (intrest vorig jaar werd in de belegging gestoken), dus 525 / 10.500 = 5%

Conclusie: het rendement is in principe in deze gevallen gelijk aan de intrestvoet (ik ga niet in op de weinige uitzonderingen om je niet in verwarring te brengen).

Rendement van obligaties

Het probleem bij obligaties is dat de uitgifteprijs niet steeds de prijs is die je krijgt bij verkoop. De terugbetalingprijs kan hoger, gelijk of lager zijn dan het geleend bedrag (respectievelijk boven, a en onder pari). Om het rendement te berekenen zijn er 3 methodes:

1) Het couponrendement (current yield):

Hiervoor neemt men de verhouding tussen de jaarlijkse coupon en de huidige marktprijs. Zo bedraagt het couponrendement van een 15-jarige, 7% couponobligatie met een faciale waarde van 1.000 die aan 769,40 verkocht wordt 70 / 769,40 = 9,1%. Dit wordt vaak gebruikt en is zeer eenvoudig (is eigenlijk hetzelfde als bij onze staatslening), maar houdt geen rekening met de tijdswaarde van geld evenals met potentiële kapitaalwinsten of –verliezen.

2) Yield to Maturity (actuarieel rendement, effectief rendement):

De Yield to Maturity (YTM) is die rentevoet die de huidige waarde van de kasstromen van de obligatie gelijk maakt aan de marktprijs. Als formule geeft dit:


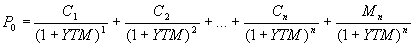
Met C₁ tem C_n de jaarlijkse coupons
P₀ de huidige marktprijs
M_n de mantelwaarde

Stel een nulcoupon-obligatie (dus zonder coupons) dan blijft enkel de laatste term over (alle waarden van C zijn 0, dus al die termen vallen weg).



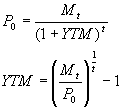
Een obligatie met een mantelwaarde van € 100.000 en een resterende looptijd van 2 jaar met een huidige waarde van 85.165,93 zal bijgevolg een YTM van 6,5% hebben. Wanneer er wel coupons zijn is het echter heel wat moeilijker. Neem bvb een obligatie met nog 5 jaarlijkse coupons. Dit impliceert het oplossen van een 5de-graadsvergelijking. Daarom zal je hiervoor trial-and-error moeten gebruiken. 

Nemen we bijvoorbeeld een 5% couponobligatie die een resterende looptijd van 3 jaar heeft. De nominale waarde van de obligaties is € 1.000. Als de prijs van deze obligatie € 970 bedraagt, zal de YTM in elk geval hoger dienen te zijn dan de couponrente. Immers ware de YTM gelijk aan de couponrente, dan zou de obligatie a pari (tegen de nominale waarde) noteren. Indien we als eerste gok een YTM invullen krijgen we een prijs van 947,51. Deze prijs is lager dan de marktprijs wat erop wijst dat we een lagere YTM dienen te nemen. 6% geeft een prijs van 973,27. Nu weten we dat het rendement tussen 6 en 7% ligt. Na enkele verdere pogingen kom je dan uit op 6,1249%. In Excel kan je dit ook berekenen met de functie IR(range, startwaarde). Ik geloof dat je voor range dan de jaarlijkse geldstromen moet ingeven. 

Je kan het rendement ook berekenen via het totale horizonrendement. Dit is vooral nuttig om meerdere beleggingen te vergelijken. Ik ga hier niet verder op in, want deze methode is intuďtief moeilijker te begrijpen. De vorige 2 methodes moeten in principe volstaan.

Rendement van aandelen

De meest courante definitie definieert het rendement op aandelen als de procentuele verandering van de prijs van een effect over een bepaalde tijdspanne:


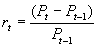
Stel: een aandeel heeft op 30 juni een koers van € 95,50, 1 dag later staat het aandeel aan € 94,10 genoteerd. Het 'dagelijks' rendement is dan (94,10 – 95,50) / 95,50 = -1,466%.

Nu, in de praktijk werd die dag het dividend uitgekeerd voor € 1,40. De aandeelhouders kregen dus € 1,40, wat ervoor zorgde dat de koers daalde met € 1,40. Voor de aandeelhouders was het een nuloperatie. Dit zou dus een rendement van 0% moeten geven. Daarom wordt de formule dus aangepast als volgt:


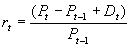
Deze formule kan je evengoed gebruiken om wekelijkse, maandelijkse of jaarlijkse rendementen te berekenen.
 
In de praktijk gebruikt men ook vaak continue rendementen. Het continue rendement wordt berekend als:
R_t = ln(P_t + D_t) – ln P_t-1
 
Voor kleine rendementen (10%) zijn ze een goede benadering van de gewone rendementen. Ze hebben echter 2 belangrijke voordelen. In de eerste plaats geeft een niveauverandering aanleiding tot hetzelfde rendement of het nu om een stijging om een daling gaat. Stel dat een prijs van 100 naar 110 evolueert, dan geeft deze wijziging een rendement van ln(110/100) = 9,53102%. De omgekeerde beweging van 110 naar 100 geeft ln(100/110) = -ln(110/100) = -9,53102%. Reken dit zelf eens uit met het gewone rendement. Het tweede voordeel is dat je gemakkelijk kan omrekenen naar grotere periodes. Als je alle dagelijkse continue rendementen optelt, heb je het wekelijkse rendement.

Gebruikt materiaal:
M. De Ceuster
Cursus Financiële Economie
Universiteit Antwerpen

Ik begrijp dat dit allemaal wat overweldigend kan overkomen. Dus als iets onduidelijk is, of als je over iets wat meer wil weten, laat dan maar wat van je horen.

Groetjes,

dinsdag 17 februari 2004

©2001-2024 WisFaq