De inverse matrix

De inverse matrix.....in het boek moderne wiskunde A1 deel 3, hoofdstuk A@ uitgelegd als: Voor het terugrekenen met matrices kun je de inverse matrix gebruiken. Maar hoe? Ik snap niet hoe je zonder grafische rekenmachine aan de inverse matrix komt en wat je ermee kan...

Willem
Leerling bovenbouw havo-vwo - zaterdag 9 maart 2002

Antwoord

Stel je hebt een matrix A. Dat is de inverse matrix A^-1 de matrix waarvoor geldt:
AA^-1=I (I=eenheidsmatrix)

Dit kan alleen bij 'vierkante' matrices waarbij de determinant¹0. De bedoeling er van is dat je een matrixbewerking om kan keren:
C=MA
Hoe krijg je als je C weet M weet terug?
M=CA^-1=MAA^-1=M

Om 'zonder' grafische rekenmachine de inverse matrix te vinden gebruik je deze formule:

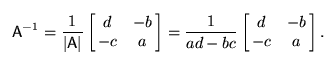
Hierin is |A| de determinant.

Voorbeeld



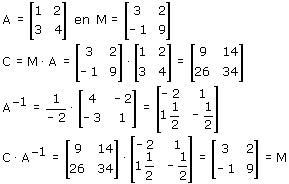
Voor een matrix van 3x3 wordt het al snel ingewikkeld, maar daar zijn weer aparte methodes voor.

Zie Matrix Inverse

zaterdag 9 maart 2002

Re: De inverse matrix

Re: De inverse matrix

©2001-2024 WisFaq