Algoritme netwerk

de snelste weg in een vierkant rooster van 25 x 25, dan schijn je te moeten doen :6,2 x 10¹⁵ keer twee getallen optellen. Hoelang doet een computer daarover? en hoe komen ze bij 6.2 x 10¹⁵? En hoe reken je met behulp van algoritmes de kortste route in een n x m netwerk?

alvast bedankt!

Toelichting:

In een rooster van 3 x 3 hokjes, is de rechtsboven hoek punt B, en de linksonder hoek punt A

Hoe reken je uit wat de snelste weg is van punt A naar B, en hoe reken je dit uit met een groter netwerk (bv 25 x 25). En hoe kom je erachter wat de snelste route langs alle wegen is?
En als je een computer het uit zou laten rekenen, zou dat sneller gaan? En hoe lang zou hij er dan over doen ongeveer?
En aan de hand van dit figuur:




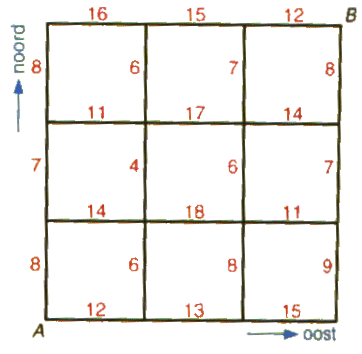
Hoe werkt dit algoritme, en hoe kom ik erachter wat de ontbrekende stappen (4 en 5) zijn in dit plaatje?

Ik hoef geen kant en klare antwoorden, de manier waarop zou al aardig wat zijn...
Alvast bedankt

Jonata
Leerling bovenbouw havo-vwo - maandag 2 februari 2004

Antwoord

Aardig sommetje. Ik wil wel heel graag weten waar dit uit is gehaald.

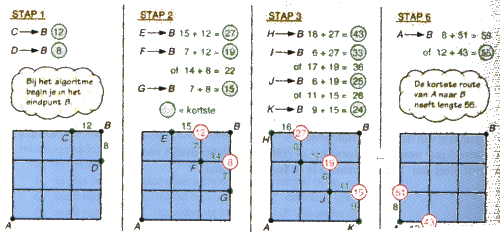
Stap 1: Je begint bij het eindpunt B. Nu ga je van alle punten die een verbinding tot B hebben de (kortste) afstand tot B bepalen. Deze punten C en D krijgen als waarde de kortste afstand tot B dus:
De waarde van D is 8 en die van C is 12.
Stap 2: Pak nou alle punten (E,F,G) die een directe verbinding hebben tot een van de punten die je al gehad hebt (C of D)
Bij E is de kortste afstand tot B via C = de waarde van C + plus afstand van EC = 12+15=27, E krijgt waarde 27.
Nu vanaf F naar B: kan via C met afstand 19 en via D met afstand 22. Kies nu de kleinste waarde als waarde voor F, dat wordt dus 19 (voorstellend de kortste route vanaf F naar B).
enzovoorts ..............
Voor de snelste route vul je gewoon tijden in in plaats van afstanden.
Piece of cake !!

Tja zo werkt dat.......of....... werkt dat zo niet ??

Leuk die experimentele opgaafjes in wiskundeboeken. Nog "leuker" als de makers het zo gek willen verzinnen dat ze er zelf blijkbaar ook niets meer van snappen. Want dit algoritme is namelijk FOUT.

Dat kun je ook makkelijk zien als je de opgave een beetje verandert


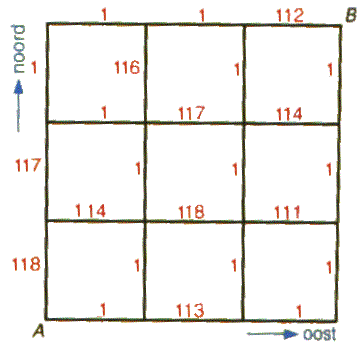
Probeer maar uit !! Another one bites the dust !
O ja, er zijn andere algoritmen die wel echt werken. Waarbij je ook in zo'n rooster wel kunt zeggen hoeveel berekeningen het algoritme nodig heeft. Ik kan je wel verklappen dat een computer in een rooster van 25x25 punten met zo'n algoritme in een flits de oplossing heeft....... Het aantal bewerkingen ?? Ik schat een paar duizend en zeker niet iets met 15 nullen !!

Leuk om dit allemaal uit te zoeken voor je PO'tje...... Hehe, het laatste plaatje kun je er alvast inzetten. Succes verzekerd !!

Met vriendelijke groet

JaDeX

woensdag 4 februari 2004

Re: Algoritme netwerk

©2001-2024 WisFaq