Methode van Cardano: Van 6 naar 3

Beste mede-beantwoorders,
Heb me de laatste tijd weer eens verdiept in de methode van Cardano, omdat iemand mij op een fout in mijn werkstuk hierover attandeerde.
Heb dat probleem opgelost, maar wil nog voor de volledigheid iets toevoegen.
Heb vanalles getracht te doen, maar kwam er maar niet uit.
Het probleem wat ik wil oplossen is het bewijzen dat de 6 verkregen oplossingen er eigenlijk slechts 3 zijn.
Bij de methode van Cardano maakt men namelijk eerst gebruik van de abc-formule en vervolgens neemt men hier de derdemachtswortel uit. De abc-formule geeft altijd twee opties (de + en de -) en een derdemachtswortel altijd drie.
Hoop dat iemand hier wat van weet.

M.v.g.
PHS

peter
Docent - woensdag 14 januari 2004

Antwoord

dag Peter

Zie onderstaande link voor de notatiekeuze.
a³ moet dus voldoen aan een van de twee oplossingen van de kwadratische vergelijking.
Noem r de oplossing met + voor de wortel
Noem s de oplossing met - voor de wortel
Het leuke is:
als a³ = r, dan is -b³ = s:

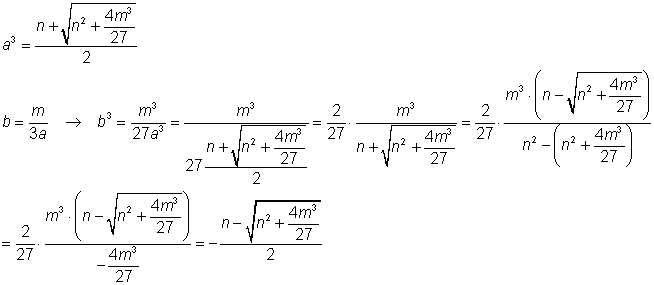
Noem a1, a2 en a3 de drie oplossingen van a³ = r
en b1, b2 en b3 de drie oplossingen van -b³ = s.
De drie waarden van a1-b1, a2-b2 en a3-b3 zijn de oplossingen voor x.
Als je daarna de drie oplossingen van -b³ = r aftrekt van de drie oplossingen van a³ = s, vind je precies dezelfde oplossingen.
groet,

Zie Quadratic, cubic and quartic equations

woensdag 14 januari 2004

©2001-2024 WisFaq