Consumentensurplus door integratie

Op een lokale markt wordt de vraagfunctie naar pinda's gegeven door
p=(30q+7000)/(q+100)
0q500
Hierin is de prijs in guldens per 100 zakjes en q is het aantal gevraagde zakjes. De aanbodfunctie voor dit produkt wordt gegeven door
p=5Öq
0q500
Bepaal de consumptiesurplus en produktiesurplus in de evenwichtsituatie. (het evenwichtspunt is p=50)

moppet
Student hbo - maandag 12 januari 2004

Antwoord

Hoi Moppetje,

Eerst kan je altijd best een grafiek tekenen van de situatie en de benodigde oppervlakte aanduiden. Zodat je gemakkelijk kan zien hoe je via integralen aan deze oppervlakte kan komen.



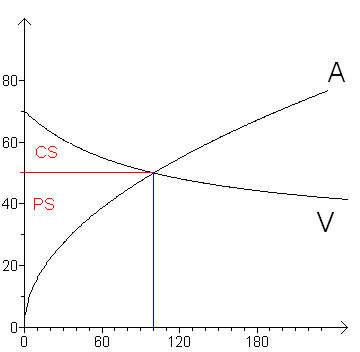
Je ziet dan meteen ook dat het evenwichtspunt bij een prijs van 50 is en een hoeveelheid van 100 (mathematisch door vraag en aanbod aan elkaar gelijk te stellen).

Consumentensurplus (CS)

Het consumentensurplus is het gebied onder de vraagcurve maar boven de evenwichtsprijs van 50. Eerst moet je dan de bepaalde integraal nemen van 0 tot de evenwichtshoeveelheid 100 van de vraagfunctie. Maar dan heb je het gehele gebied onder de vraagcurve tussen een hoeveelheid van 0 en 100. Daarom moet je die onderste rechthoek (onder de evenwichtsprijs) ervan aftrekken. Je kan deze snel berekenen als de oppervlakte van een rechthoek: basis x hoogte = 50 * 100 = 5000. Of de bepaalde integraal bereken van 0 tot 100 van p = 50. Maar het is vooral de vraagfunctie die niet zo eenvoudig te integreren is. We moeten de teller immers eerst nog wat herschrijven zodat het wat eenvoudiger wordt.

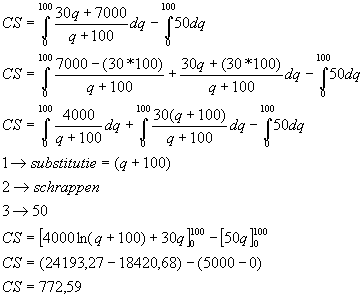
Producentensurplus

Dit is gelijkaardig. Het producentensurplus vinden we door de oppervlate van die rechthoek onder de evenwichtsprijs te verminderen met de oppervlakte onder de aanbodscurve. De rest verloopt identiek.



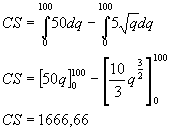
Groetjes,

Zie vraag 11798

dinsdag 13 januari 2004

©2001-2024 WisFaq